RL2: Value estimation

在RL1中，介绍了MDP和基于其建模的动态规划方法。然而，这种方法十分依赖于对于整个环境和模型的充分了解；而在更多的无法明确地给出状态转移和奖励函数的情况下，我们就会更加依赖于直接从获得的数据中学习相应的价值与策略。 >在这种情况下，智能体只能和环境进行交互，通过采样到的数据来学习，这类学习方法统称为无模型的强化学习（model-freereinforcement learning）

1.蒙特卡洛方法

1.1 总体思路概述

蒙特卡洛方法（Monte-Carlo methods，简称 MC） 在数学上是指一种依赖于大量随机抽样得到数值结果的方法；而在RL中，其思想为使用策略π从状态s采样N个样本，并使用经验均值累计奖励近似期望累计奖励(也就是V)的方法

1.2 具体实现方法

一般来说，在实现蒙特卡罗方法的时候，我们需要使用固定的策略模拟若干个回合并且相应记录累计奖励，对于没有明确终止条件的情况，一般规定一个T为应用策略π采样的时间数。（只有有限MDP可以模拟到结束）之后，通过不断累加总的采样次数N(s)(表示从状态s开始采样)和总的累计奖励V(s),当N(s)足够大的时候，就可以利用V(s)/N(s)来估计状态s的价值。

1.总结一下，Monte-Carlo就是提供了在对环境完全未知的情况下通过多次模拟算出V^π(s)的方法，这可以 “帮助你理解，在某一状态下，执行策略的长期回报是什么。这对于强化学习的策略评估非常有用，尤其是在不知道环境动态的情况下。” 2.在实操的时候，为了节约计算量，直接使用增量的方式进行更新 第二部分的更新公式为后面Q-learning要使用的增量公式，数学推导也很简单，具体作用往下看

有些时候，会碰到更加复杂的情况：有可能环境不仅转移概率为止，而且可能是非平稳环境（Non-Stationary Environment） ，即环境的转移概率和奖励函数会随时间而改变。在这种时候，按照之前的方法采用蒙特卡洛显然不适用，因此采用以下的滑动窗口技术： 在这个时候，仍然像之前一样算出每一次采样之后的V值，然后与先前不同的是，采用一个固定长度的“窗口”进行计算：每次纳入一个新的值的同时删除最老的。在这个时候，由于窗口长度固定，因此增量的改变也变成了乘上固定的系数α，其大小为窗口长度的倒数。(和learning rate一点关系都没有！)

那么环境不断变化，窗口什么时候才要停下来呢？gpt这么解释： > 在非平稳环境中，环境是不断变化的，因此滑动窗口和蒙特卡洛方法的 停止条件 和 估计收敛 是相对复杂的。关键在于平衡 适应环境的变化 和 获得稳定估计 之间的关系。在 非平稳环境 中，估计值是不断调整的，因为环境的状态转移和奖励会随时间变化。 有点抽象，后面尽量结合例子理解（大概意思是，会根据环境不断变，就让它一直跑下去就行）

同时可以比较容易看出，可以使用蒙特卡罗方法进行估计的前提是两个状态之间转移的奖励必须是已知的，否则无法进行计算！

2.时序差分方法

2.1 总体方法概述

时序差分方法（ Temporal Difference methods，TD） 是另外一种模型无关的，直接使用经验学习的方法。时序差分方法的核心公式如下： 在时序差分中，我们通过当前行为带来的即时奖励以及下一个回合的V值与γ（也就是，对于未来的估计值）来更新当前状态的价值V

这里使用学习率 α 来控制更新大小的大小，是为了避免产生过度更新的问题，比如更新值过大导致来回震荡，而加上一个系数可以保证平滑更新

2.2 时序差分 vs 蒙特卡洛

（1）从上面的定义就可以看出，时序差分方法在每一次执行动作之后都会利用下一个状态的V值更新（每一步后可以进行在线学习），而蒙特卡洛则需要跑完一个回合之后才会利用累计奖励对于V(s)值进行更新 （2）很容易知道蒙特卡洛方法一定是无偏估计，而时序差分方法由于使用的就是下一个状态的猜测值V(s_t + 1)而不是该策略下的真实值V^π(s_t + 1)。因此，TD是有偏估计。 （3）时序差分方法对于初始值更加敏感，而蒙特卡洛方法对于初始值不敏感 （4）蒙特卡洛方法得到的结果的方差更大，而时序差分方法得到的结果方差更小 总结下来如图所示：

3. 资格迹方法

3.1 总体方法概述

如果说把使用窗口的蒙特卡洛方法中的窗口大小倒数α看作类似于“学习率”的参数，那么前面三个方法的关系可以这样概括：时序差分是只参考当前下一步的估计方法，资格迹方法是参考下面若干步的多步时序差分方法，而蒙特卡洛方法则是参考未来无限步（直到回合结束）的方法。

因此，资格迹方法（Eligibility Traces methods） 可以看作是前面两种方法的一个平衡，其平衡了方差和偏差的关系，是一种比较折中的方案。依葫芦画瓢得到如下的公式：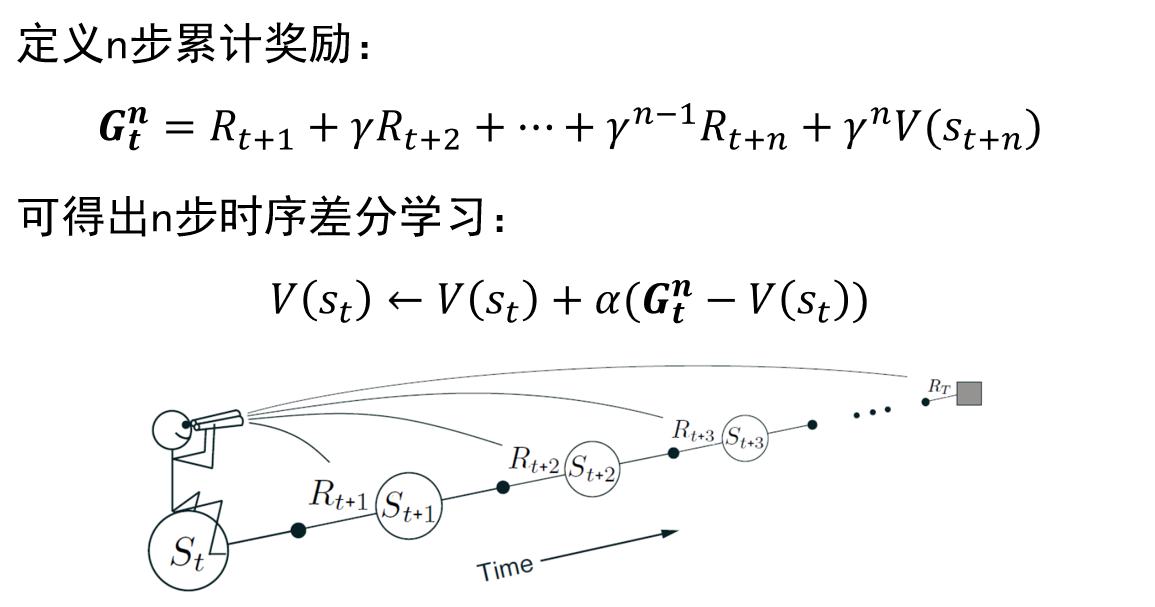

3.2 具体实现

3.2.1 TD − λ 方法

所谓的 TD − λ方法，是指使用一个超参数λ 进行控制后续使用的各个阶段G的权重，具体如下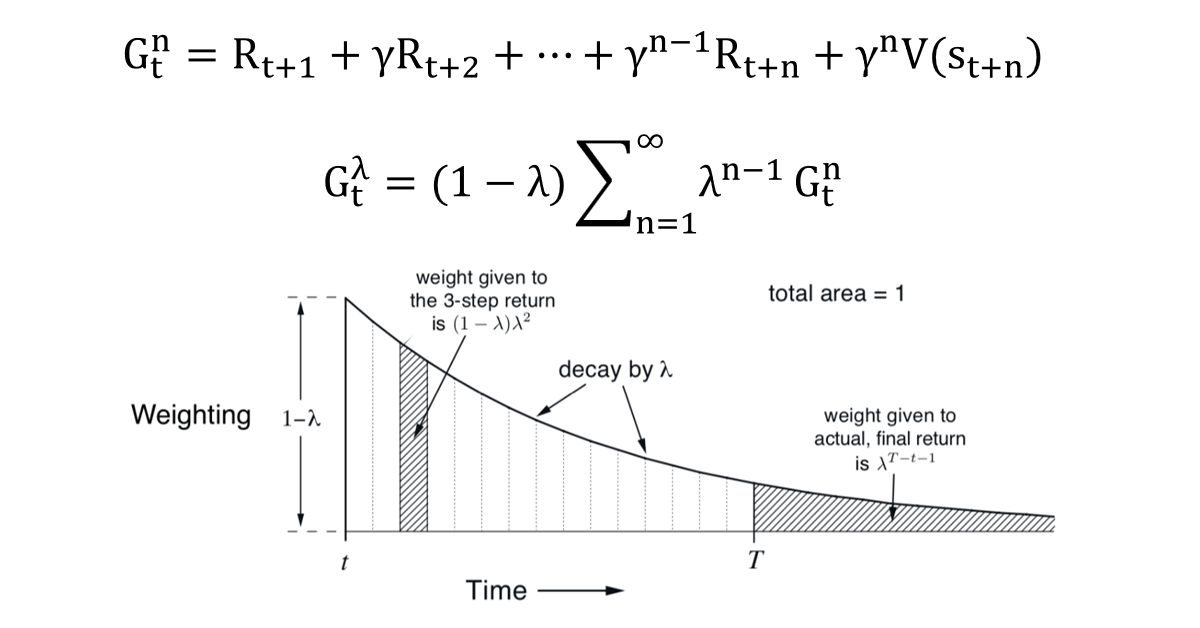： 解释一下：G_tⁿ 指的是（上面所说的）考虑了之后n步具体奖励的资格迹方法；第二个公式实际上是一个加权平均（注意到：λ+λ² +…+λⁿ =$\frac{1}{1 - \lambda}$ ）。可以看到，距离现在时间越远的远期奖励权重会越来越小，而参数λ控制着这个权重衰减的速率。

这种方法较好地平衡了MC和TD，其不仅会有更快的收敛速度（相比于MC），而且平衡了偏差和方差之间的关系；同时，保留了大量的历史信息的加权结果，使得对于价值的估计更加全面。

下面是两张直观反映TD − λ方法的图片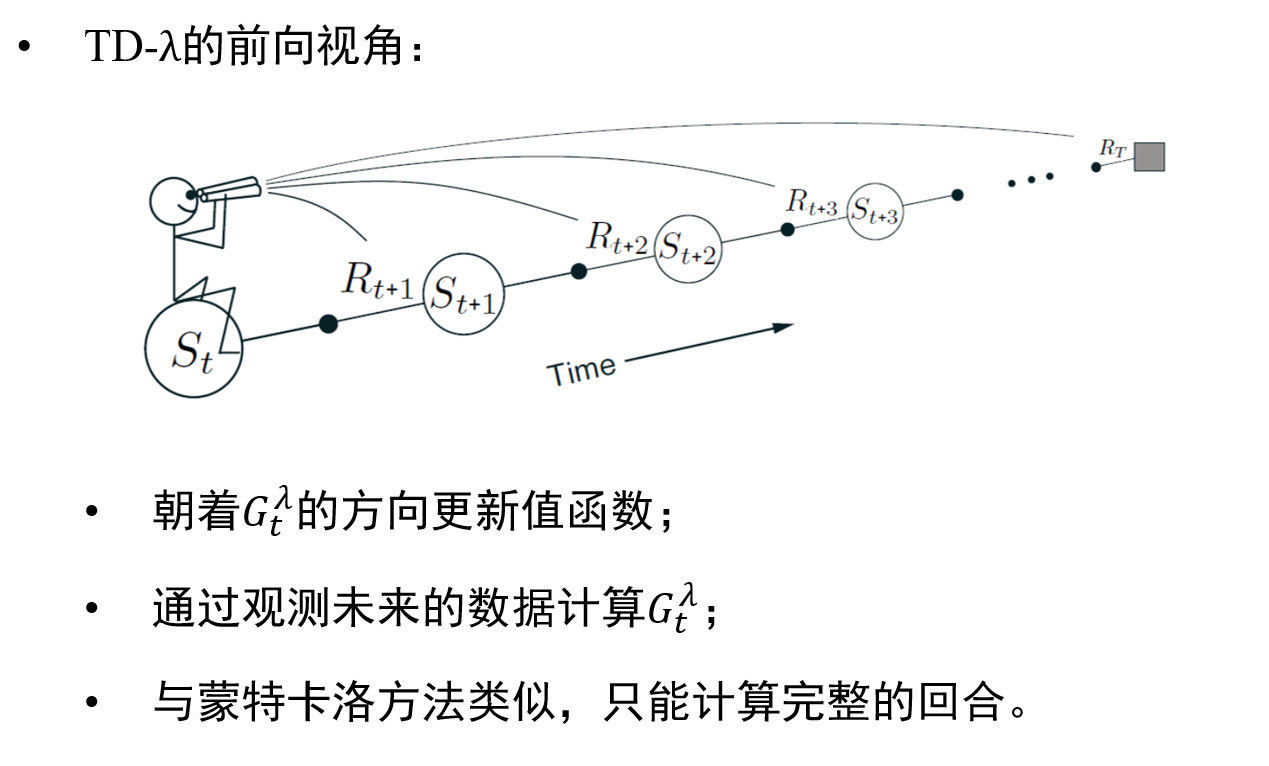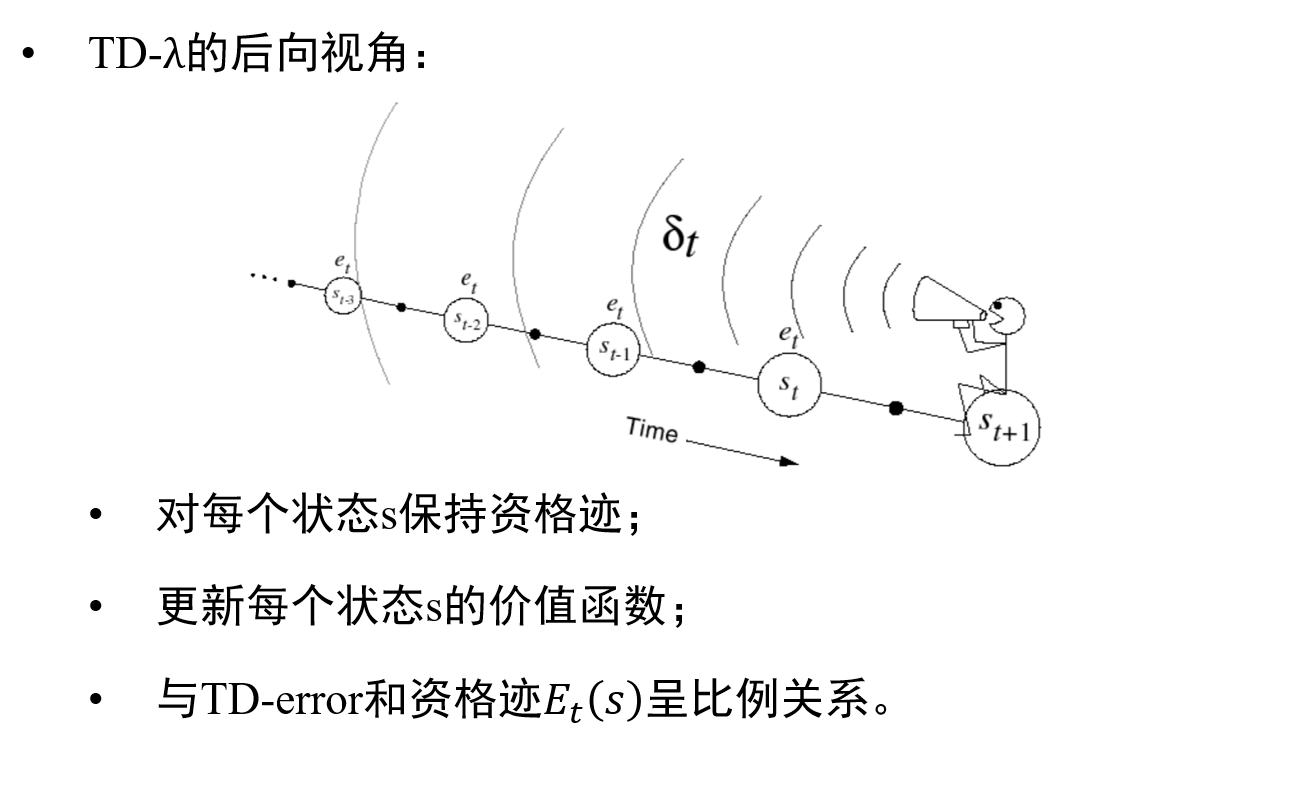： 但是暂时不是很理解具体的意思，不知道这个”后向视角“具体是怎么结合的

4. 表格型时序差分方法：SARSA & Q-learning

4.1 核心思想

强化学习的核心部分便是策略评估和策略优化 （recall：之前dp的策略迭代和策略评估），具体都在下图中有所指出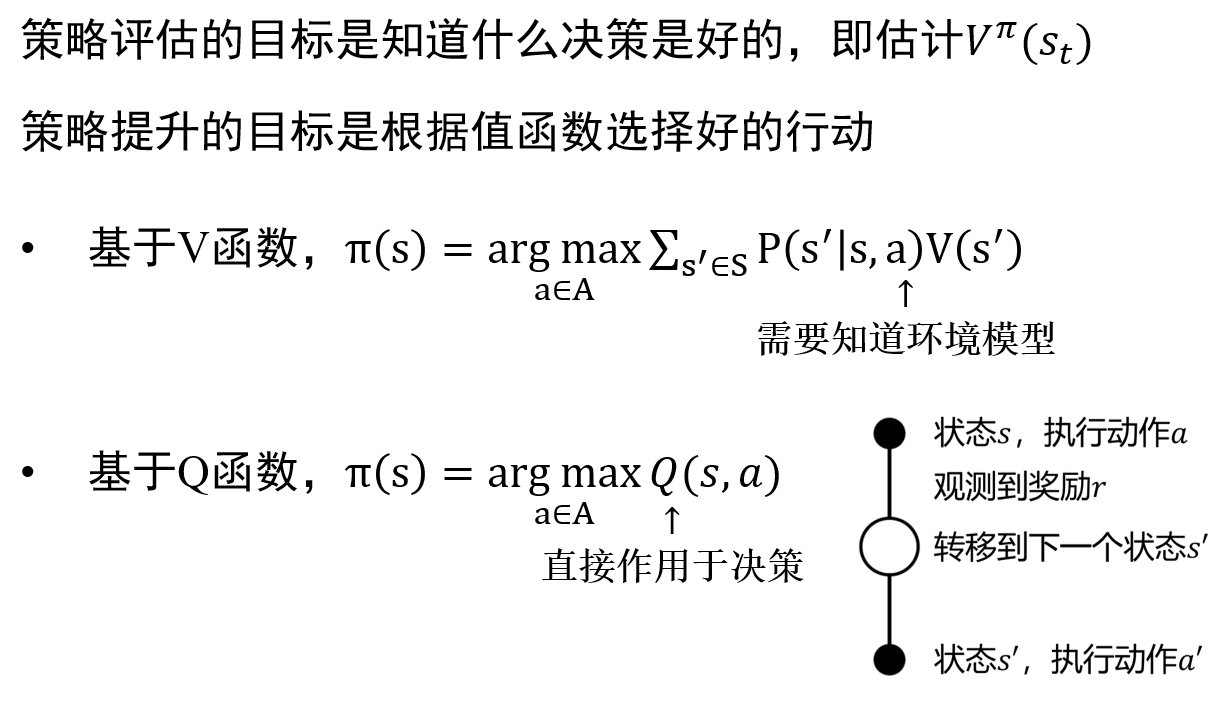： 也就是说，策略评估就是估算出V,(也就是之前几个部分在做的)，之后再根据算出来的V^π(s)，来选择最好的策略（动作）

4.2 SARSA

4.2.1 总体方法概述

所谓的SARSA，指的是State-Action-Reward-State-Action。先来看一段伪代码，直观反映了这个方法的运行步骤： 作为背景，首先介绍 ϵ − greedy 方法：这是一种在强化学习中常用的平衡探索与利用的手段。在每一个时间步中，agent都会以ϵ的概率随机选择一个动作（实现对未知的探索），以1 − ϵ的概率选择当前的最优策略（贪心，实现对现在的利用）
接着，基于上面策略评估与策略优化的思想，SARSA分为如下几个步骤实现： step1： 初始化参数值，包括初始化各个Q(s, a)的值，以及初始化每个步骤用于选择的ϵ初始值

step2： 从初始环境s₀开始，在每一个状态s处，按照ϵ-greedy策略进行选择动作a_t（即，可能选择当前的最佳，也有可能随即探索），并且根据这个行为观察奖励R；随后进入下一个状态s′,并且再利用一次ϵ-greedy策略进行选择动作a′，并且读取对应的$Q(s’,a’)的值

step3： 利用上途中的公式，更新Q(s, a)的值；并且一直重复这个过程，直到Q值收敛或者状态结束

4.2.2 原理是什么？

对于SARSA的原理，可以把它看成是针对当前策略的一个 TD的更新，因为在更新公式中，可以把 R + γQ(s′, a′) 这一项看作是对于当前策略奖励（更）准确的值（因为多向前跑了一项），而 Q(s, a) 则可以看作是当前状态下对于这样一个行为结果的一个预测，因此对于两者给上一个学习率系数就可以实现学习的过程。

SARSA的一个性质是，随着训练的进行，模型会越来越快抵达最后的“目标”，即最后比较接近的预测值。

4.3 Q-learning

4.3.1 基本方法概述

SARSA是一种典型的 on-policy 方法，即，在进行学习过程中使用的策略就是智能体使用的策略；而与之不同的是，Q-learning是一种 off-policy 方法，这个的意思是，学习的策略与当前使用的策略不同，而是先“贷款”了未来会学习到的最优策略进行优化。 Q-learning的核心是如下的这个公式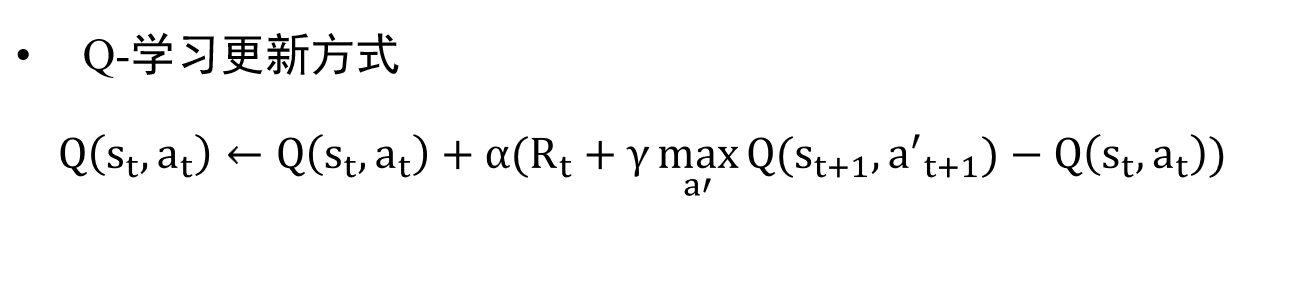： 可以注意到，和之前的SARSA不同，这里更新的下一步得到奖励使用的是“期望来到下一个状态之后所取得的最优步骤（即为最大的奖励），其他的结构是一样的。（recall之前的SARSA，区别就是SARSA只会以ϵ的概率随机选择状态s′最优的动作）

4.3.2 具体实现方法

可以把Q-learning看作简单版本的SARSA，其每一步都会默认选择最优的策略（而非按照一定的概率）来更新数值，根据数学的定理其一定会收敛到最后的最优策略Q*

这是一个直观展现Q-learning和SARSA两个不同特点的例子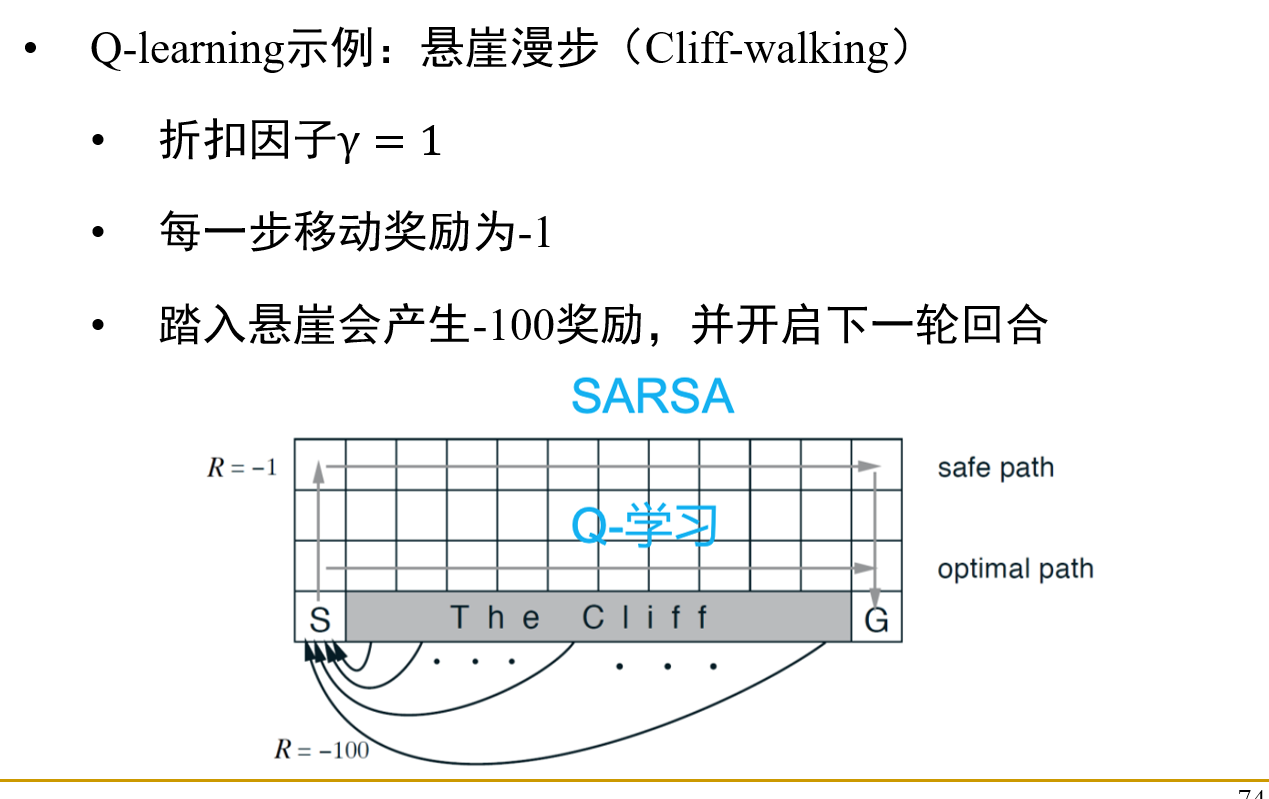： 由于Q-learning倾向于选择”最佳的“，所以其会贴着悬崖走；而SARSA会按照一个更加探索过的路线行走。

总结一下这个部分的内容：和标题一样，这个部分主要介绍了强化学习中的值估计部分的内容，从一开始的MC和TD以及资格迹是对于V值估计的三个方法，到后面的两个表格式TD对于每一个状态-动作组的Q值的估计，这个部分在RL1的基础上进一步展示了当环境对我们更为陌生的时候应该如何对于各个状态和行为的价值进行估计。