RL3：深度学习&DQN

RL3: 深度学习&DQN

这个部分的笔记主要介绍一些深度学习的基础内容，以及其与强化学习结合的DQN方法的例子。由于深度学习不是这个部分的重点，就简单梳理一下框架，具体的各个算法和函数背后的原理就罗列一下，不去深入学习了（）

1. 深度学习基础

1.1 神经元&神经网络，神经网络训练

在神经网络中，“神经元”是其中最基本的组成单位，其基本结构如下所示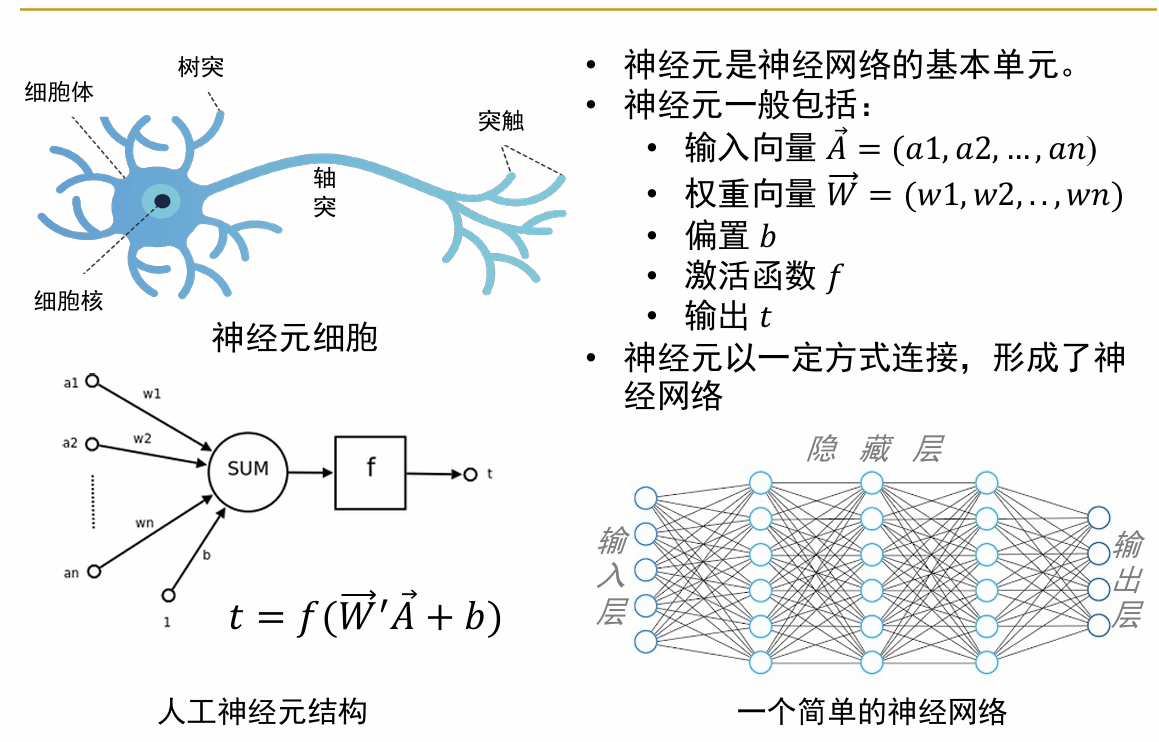： alt text 也就是说，输入了一系列有一定权重的量加上偏置值，然后经过激活函数，得到输出。有如下几个概念：（1）感知机（perceptron）：我理解感知机是一种单元的、初级的神经元（单元的网络），其包括了神经元的所有特性内容，但是最后的激活函数f一般是简单的符号函数 ，即简单的对于内容的正负进行区分。感知机只能用于处理简单的线性可分问题 ，由于其激活函数的限制，只能生成一个二分数据的超平面。对于复杂一点的情况（比如xor问题），其就无法解决。（2）激活函数：为了解决感知机无法解决的问题，现代神经网络采用了多种多样的激活函数，如图所示，用于不同的场景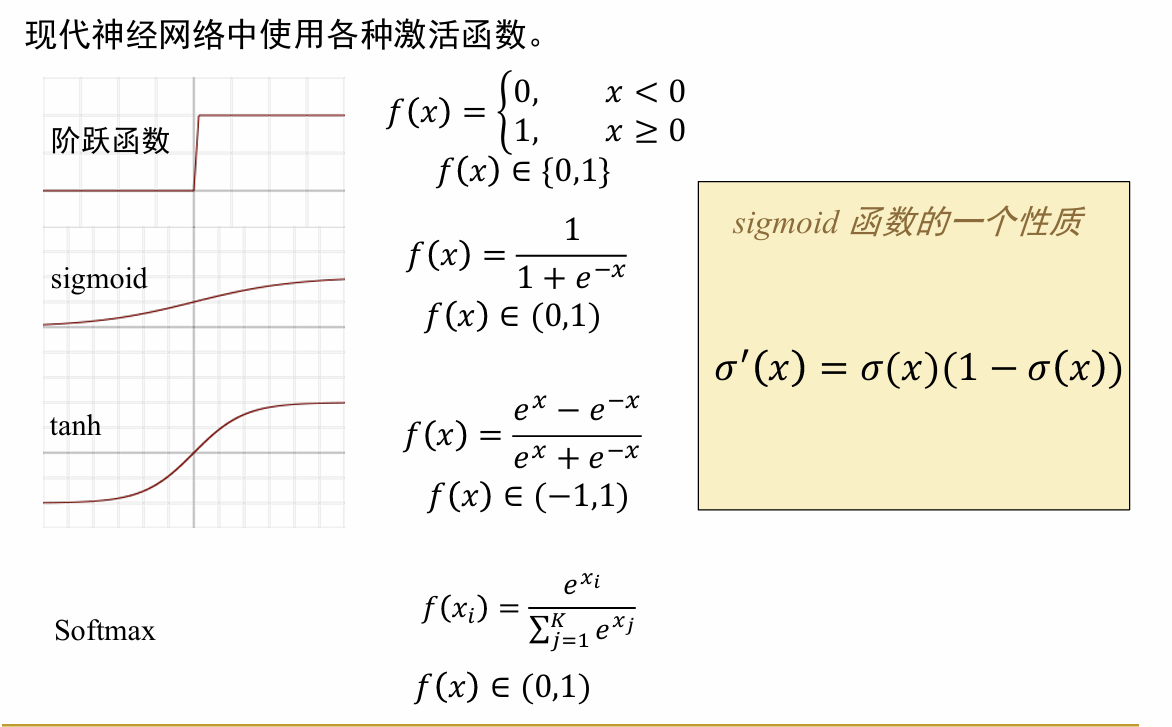 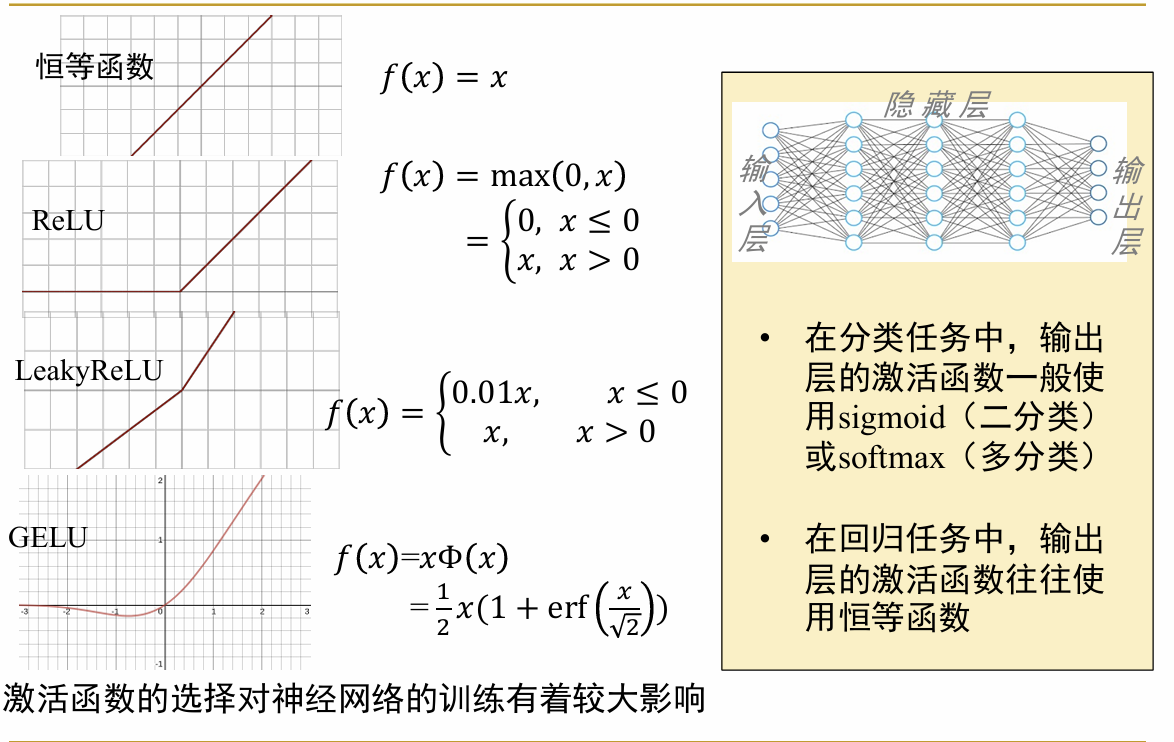alt text 以上介绍了神经网络中神经元的基本结构，下面是一些更加深入的内容（3）损失函数：损失函数是评估训练时神经网络输出的结果和真实值之间差距的函数，是用来衡量训练出的模型好坏的评估指标。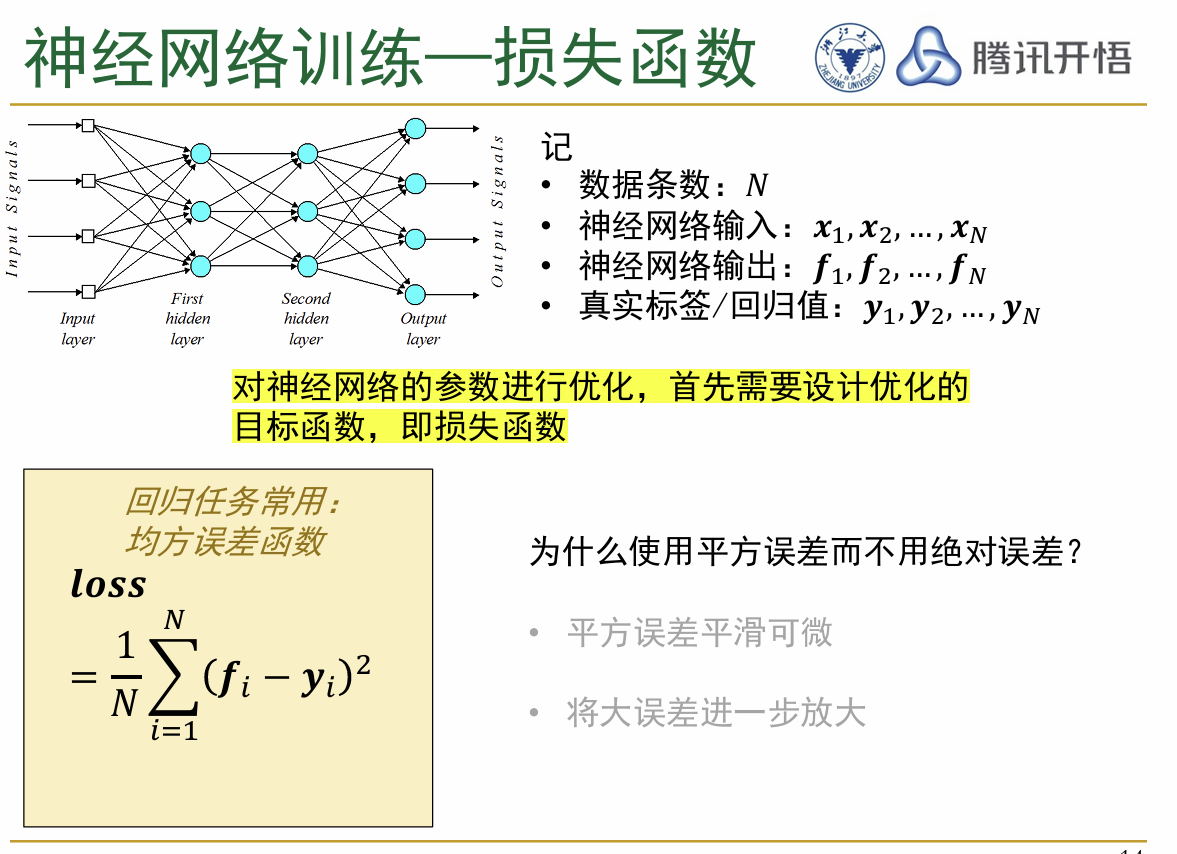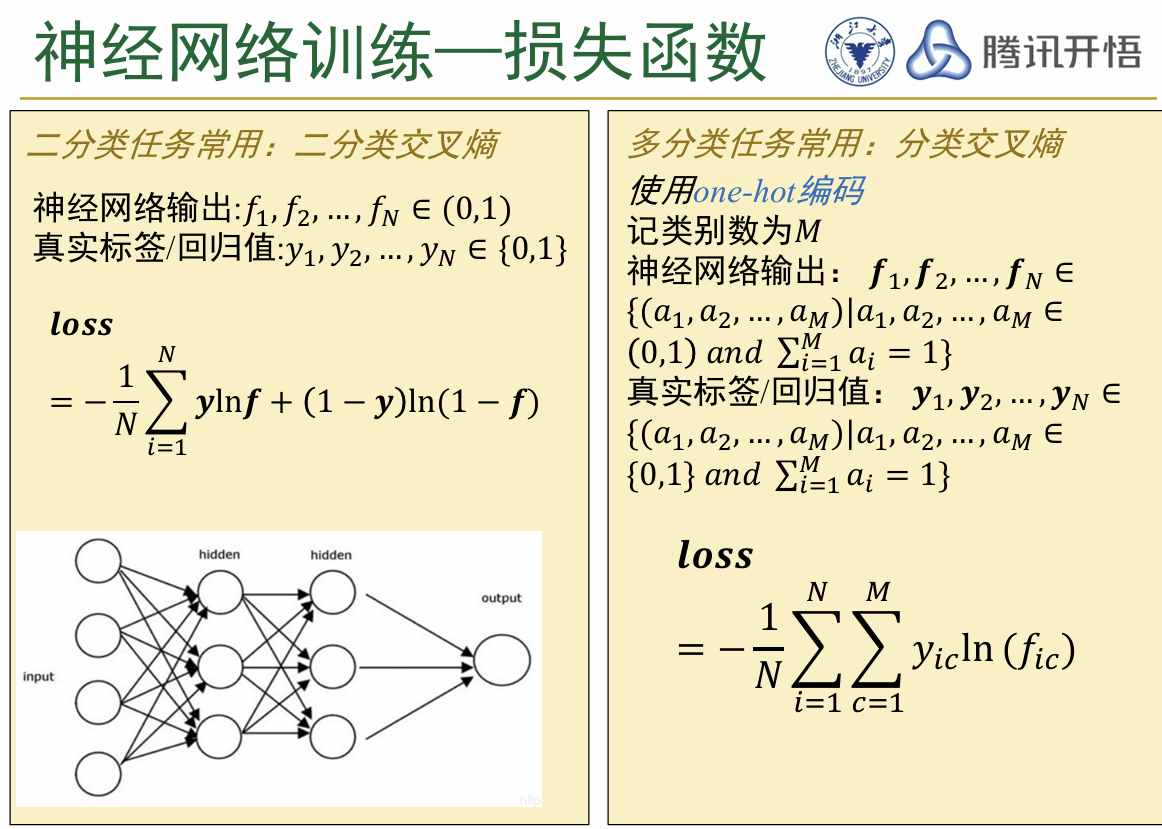根据问题的不同，分别选择不同的损失函数，如图所示 alt text

神经网络的两个主要研究对象： 回归问题（regression problem）：预测一个连续的数值输出，即根据输入的特征预测一个特定的数值。比如说，预测房价、温度，etc 分类问题（classification problem）：预测一个离散的类别，对于输入的内容将其给出一个特定的分类。比如说，邮件分类、疾病预测，etc

优化器（optimizer）：优化器是神经网络中用来更新各个参数以最小化损失函数的算法，常见的方法有梯度下降以及伴随的各种衍生的算法,如图所示
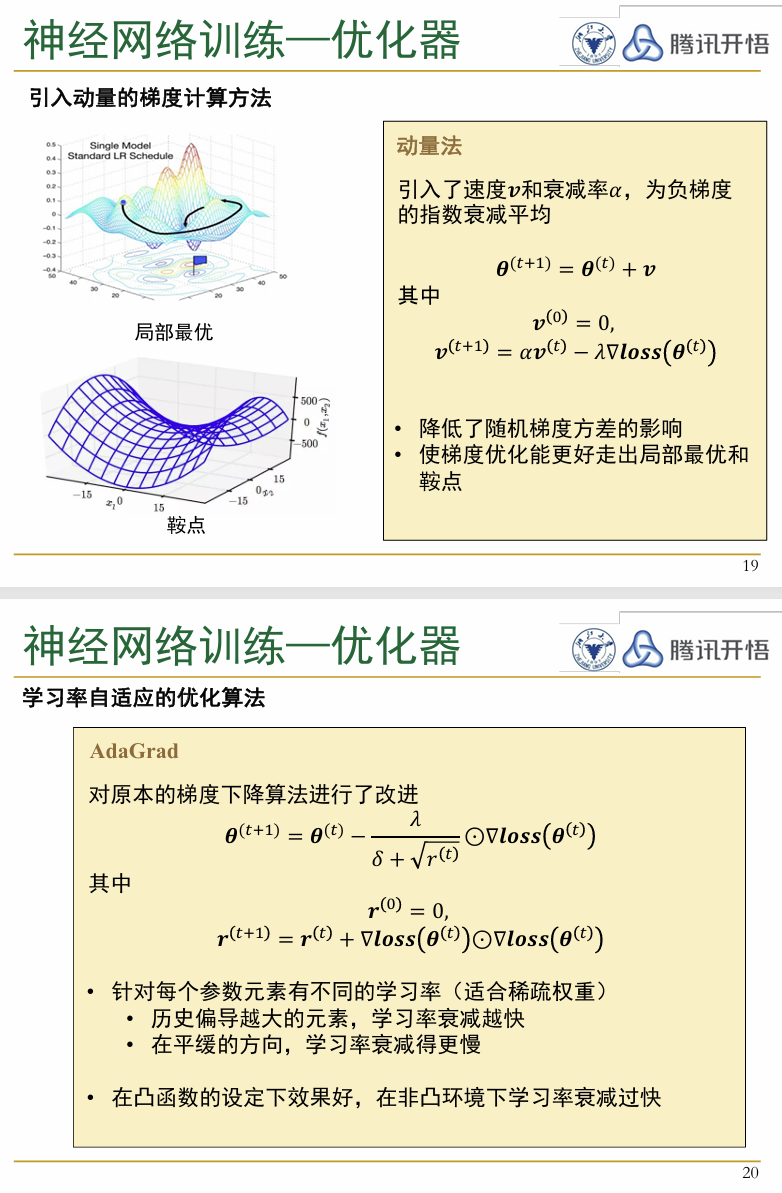
反向传播(back propagation):反向传播是在确定了上面的损失函数和优化方法之后，对于整个神经网络进行更新的过程。

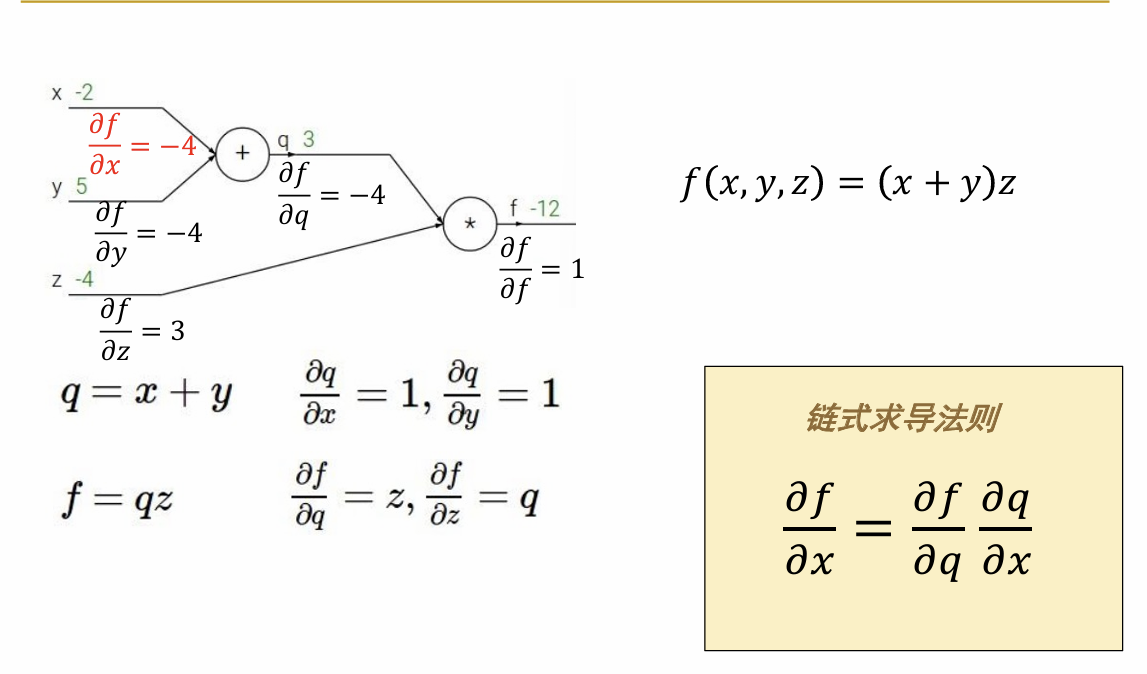以这个简单的例子为例，展示了多层神经网络中，如何利用每两层之间的函数关系与链式法则来计算最终的损失函数对于其中每一个神经元得到的梯度

在反向传播的过程中，会从输出层向前计算出每一个参数对应的梯度，然后再根据优化器选择的方法依次更新这些参数

以经典的手写数字识别（MNIST） 为例，来分析一下整个神经网络运作的流程：为了解决这个问题，搭建一个简单的三层的神经网络：（1）输入层：共有28*28=784个神经元，对应每张图片的每一个像素点（灰度），取值在1~255之间，用于输入图片的信息

（2）隐藏层：隐藏层的神经元个数不定（是一个超参数），假设有128个神经元，那么每一个神经元都会有一系列的参数，接受输入层的784个输入，并且通过线性变换和偏置的叠加得到一个值，接着经过激活之后得到对应的128个输出

（3）输出层：由于识别的是0~9这些数字，因此输出层就设定为10个神经元，每个都接受隐藏层的128个输出，之后通过神经元内的计算、激活函数激活之后得到输出，每一个输出对应得到结果是相应数字的概率。

之后，神经网络的整个工作流程如下：

（0）首先，将所有的图片进行标注之后，分为训练组和测试组，将训练组的数据投喂给模型

（1）（大多情况下，对于输入的灰度值进行归一化，将每一个值除以255，使得输入的灰度值都在0~1之间）之后进入隐藏层线性计算后，选择激活函数Relu进行激活，得到128个输出（这里使用最简单的函数Relu引入了非线性的量（2）一张图片进入输出层，同样是先线性计算，之后使用softmax函数得到十个概率值，即为测试得到的输出（3）对于每一个样例，将得到的预测结果与标签结果相比较，计算损失，接着反向传播计算梯度并且根据优化方法更新参数，完成这个图片的训练（4）重复步骤（2）和（3），直到所有图片都训练完成

1.2 循环神经网络

传统的深度学习框架对于一些“一锤子买卖”的任务处理的结果会很好，但是对于一些需要“记忆”的任务，比如说，想让其理解一个电影片段的内容，就会比较困难。因此，具有“记忆”单元的RNN应运而生。循环神经网络的基础结构如下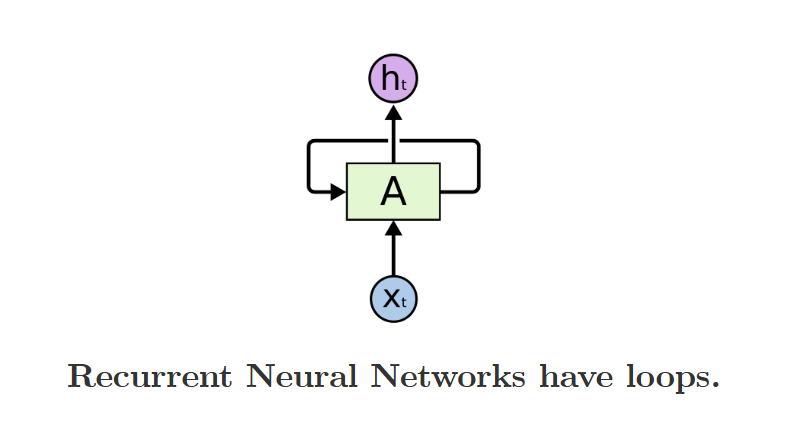： alt text 在基本的神经网络之外，有一个循环的loop；事实上，这样的结构可以看成是一系列神经网络的继承，“each passing a message to a successor”,即如下图的结构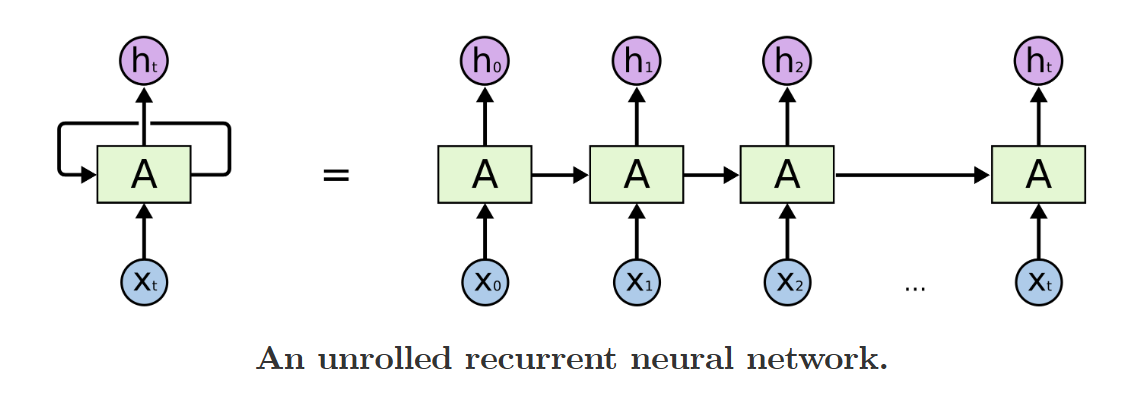：对于这个图，更详细的解释是，每一个神经网络会有一个输出值h_t，这个值会作为下一层神经网络的输入之一，并且被给予一定的权重矩阵，与这个时间点的其他输入共同作用，形成下一个时间点的输出h_t + 1；并且，RNN的特点是所有的神经网络的所有参数和权重都是完全一样的，这被称为RNN的权重共享. alt text e.g. 一个简单的例子：对于前一步的输出以及这一步的输入，简单使用一个tanh作为激活函数得到进一步的值

权重共享的好处是什么？总结下来大致如下： alt text

但是，传统的RNN往往会伴随着梯度爆炸等等的问题，因此大部分RNN取得的相关成果都于LSTM有关。

在使用RNN的时候，一个经常出现的问题就是如果相关的内容与你现在需要预测的内容距离差的很远，就会出现失效；比如说，预测一个句子的上下文，如果相关信息就在当前的这句话内，则RNN可以预测成功；然而，如果提供线索的上文距离比较远，RNN便会失效。但是，使用LSTM就不会出现这个问题！有关LSTM的内容，可以参考论文：LSTM: A Search Space Odyssey

2. DQN

2.1 问题的引入：探索与利用

比如说今晚你要到外面吃饭，那么究竟是选择自己经常去的那家还可以的饭店（“利用”）还是去边上的那家新开的饭店（“探索”）就体现了探索与利用之间的制衡关系；在强化学习中，当环境信息不完全时，即使是你对于现有状态的价值判断也可能因为样本太小而具有偶然性和不确定性，已被探索过的行为可能因为偶然概率原因被高估或者低估。

因此，在这样的背景下，什么是所谓的“最优”，如何平衡探索与利用的关系，既不轻易陷入局部最优，也不盲目探索，是需要关注的问题

2.2 一些简单的模型&方法

2.2.1 Multi-arm Bandit （多臂老虎机）

问题背景：假如你在一个赌场，面对一排老虎机（每一台都有预设的且未知的奖励分布），对于手上的有限筹码，应该如何做出抉择？一个所谓的“伯努利MAB问题”的定义如下： alt text 显然，其目的就是最大化累计奖励$\sum_{t=1}^T r_t$. 我们可以将MAB问题的最大化累计奖励转化为最小化累计悔值，我们用θ^*代表所有老虎机中获得奖励概率最大的哪一个，那么每一次得到悔值转化为θ^* − Q(a_t)，对其求和即可。