RL4：策略梯度和策略梯度算法
RL4: 策略梯度和一些策略梯度算法
首先介绍几个思想： （1）策略参数化：本质上来讲，一个策略是一个从一个特定的状态到一个动作的映射，而策略参数化则是指使用一个函数来表示一个策略，之后通过这个函数在训练的过程中不断调整来优化策略。比如说，我的参数化的策略可能是一个神经网络，根据不同的输入情况输出一系列动作执行的概率，在训练的过程中不断优化当前的方案。 策略参数化表示为 πθ(a|s)，其中θ即为用来调整优化策略的参数 （2）
1. 策略梯度介绍
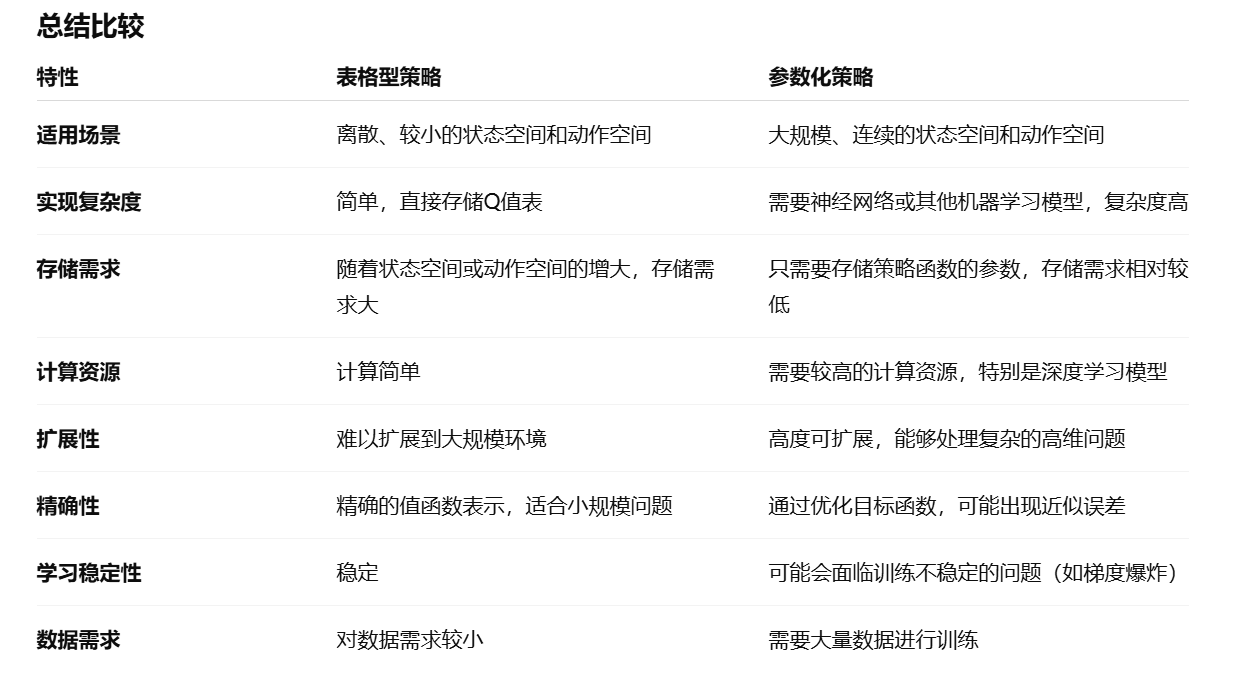在之前的RL2中，用到的一些方法都是适用于表格形式的策略，其应用的场景多为状态-动作的数量比较小的情况；而在更多的情况下使用策略梯度是另外一种可行的方案，二者的核心区别为： 
对于表格型策略，由于对于每一个状态s其均最大化了Q(s, a)，因此其一定是最优解；而根据参数化策略优化的就不一定了（可能是一个局部的最优解），二者的关系如下：
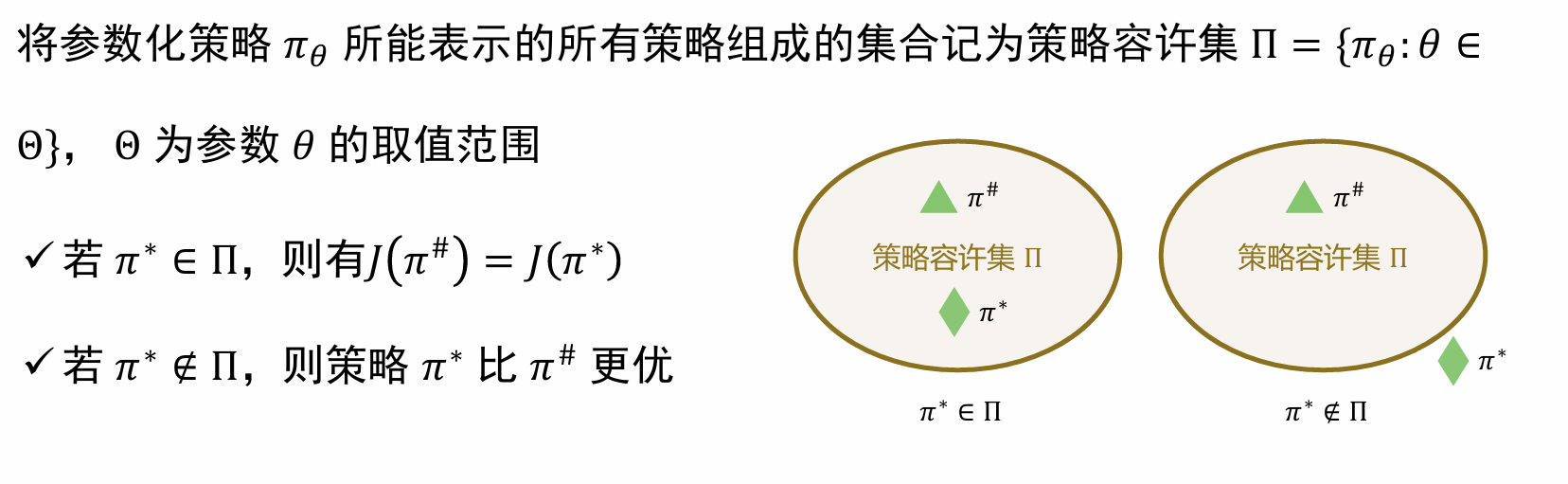总体来说，策略优化即为：寻找一个用于衡量策略的优劣的目标函数 J(θ) ，然后借助目标函数优化。 因此，对于策略梯度，其关键点就在于以下的两点： （1）如何设计合适的目标函数？ （2）如何进行计算和优化？（设定合适的learning rate 计算梯度，etc.） ### 1.1 目标函数的选择 如图所示，一般有如下的几种选择目标函数的方式，根据不同的任务和算法需求，选取不同的目标函数：
这几个公式的意义： 1.即为再当前策略下每一个状态的期望价值的按照概率分布的加权求和 2.计算的相当于是整个系统的总奖励值，具体来说：的第二个求和代表的是给定一个状态，在当前策略下各个动作奖励的概率加权和，也就是代表每一个状态所取得的期望奖励；那么前一个求和就是在当前状态分布下每一个状态对应奖励的概率加权和，也就是整个系统的总奖励 3.这是相对于轨迹而言的计算方法，相当于我在当前的策略θ下，采样一个固定的时间T之后，对于每一个出现的状态-动作序列最终得到的奖励的加权和。pθ即为出现这一串特定状态-动作的各个步骤概率的乘积。 并且，这三个函数都是所有状态的期望价值和，即排除了状态s对结果可能的干扰。
具体解释：策略无关的状态分布指的是，在长时间的实验次数中，每个状态出现的概率与你采用的策略是无关的，因此可以采用这种比较简单的假设； 而当状态分布与策略有关的时候，采用的所谓稳态状态分布指的是，在执行相当长时间后，我的各个状态的概率会不再发生明显变化。稳态状态公式也很好理解：求和的三项即为状态s下采用动作a可以转移到s′的概率，乘以当前策略下状态s采取策略a的概率，最后再乘以状态s的分布概率。也就是说，把所有状态下可能转移到s’的情况的概率进行求和，即为s’的分布概率。
1.2 计算策略梯度
1.2.1 平均轨迹回报目标的策略梯度
首先来看一下计算轨迹对应的J(θ)的策略梯度的方法：
这个计算看上去很复杂，首先明确几个事情： （1）θ是一个向量 （2）这里面用到了积分的形式，实际上可以这么理解：比如说你玩游戏，把每一个画面都看作一个状态，把向四面八方任何的移动都看成动作，那么动作和状态空间就是连续的，因此可以理解采集到的轨迹也是连续的，因此使用积分来计算总的reward （3）因此，现在的pθ(τ)是一个概率密度函数（关于τ），所有求积分即可 由于对于每一个轨迹，其rewardG(τ)是一个可以计算出的常数，本质上说是与参数θ无关的；这里注意到pθ(τ)是一个一系列概率连乘的形式，蓝色的部分就是创造出了一个对数形式的转换，结合链式法则，方便后续的操作。最后又将其写成了期望的形式。 进一步地对于这个梯度进行的展开如下：
1.2.2 平均价值回报和平均奖励回报的策略梯度
如图所示
几点需要说明的是： （1）d(s)可以看作一个在训练过程中，不断优化的“常数”，也就是说随着训练过程会不断变化 （2）recall：qπ(s, a)实际上就是一个奖励值，与具体的θ其实是无关的！ （3）最下面的hθ(s, a)指的是我的网络对于状态s下进行动作a的一个“打分”，所以使用softmax函数将其转化为正常的、易于理解的此时策略θ的采取这个行为的概率（也就是进行归一化处理） 到此为止，介绍了几种不同的策略梯度的计算方法，以此为基础延伸出了一系列近似方法和基于策略梯度的算法，核心来看就是下面的公式： 
1.3 策略梯度算法
1.3.1 REINFORCE算法
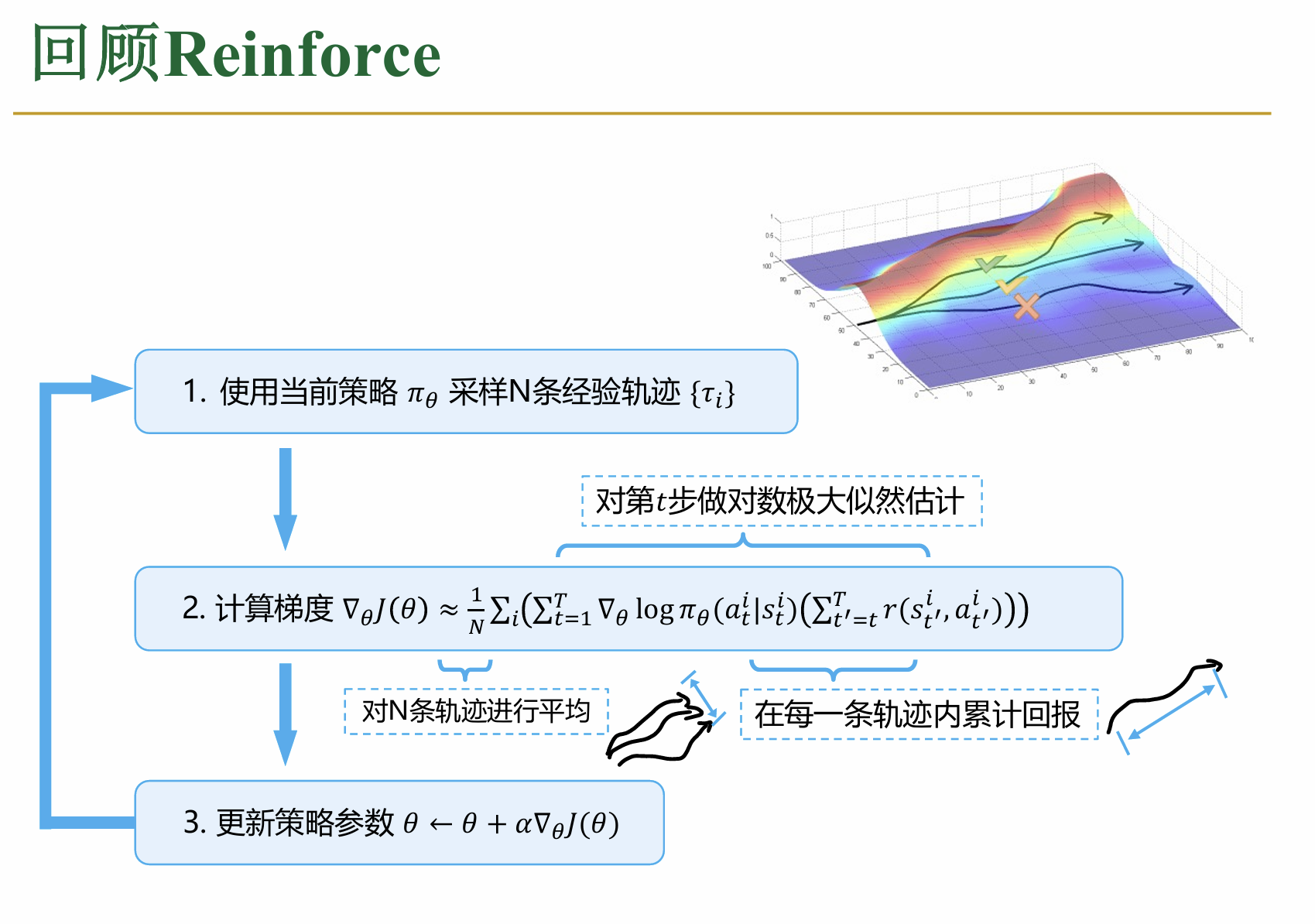
这个算法比较简单，核心思想如下图：
也就是说，要想求这个期望值，我们就直接模拟N个轨迹，之后根据蒙特卡洛方法，使用均值估计策略梯度的期望值（公式中的上标n只代表当前轨迹的编号）
对于Reinforce算法一个常用的优化方法是，添加一个baseline，即维护一个所有奖励的平均值为b，之后在上述计算的过程中，用G(τ) − b代替G(τ)，这样可以减少计算结果的方差，如图所示，并且实际上这样不会对系统的梯度值产生变化。 
1.3.2 Actor-Critic算法
本质上来说，这个算法是把基于策略与基于价值的两种算法结合了起来进行使用。具体来说，按照如下的方式进行实现：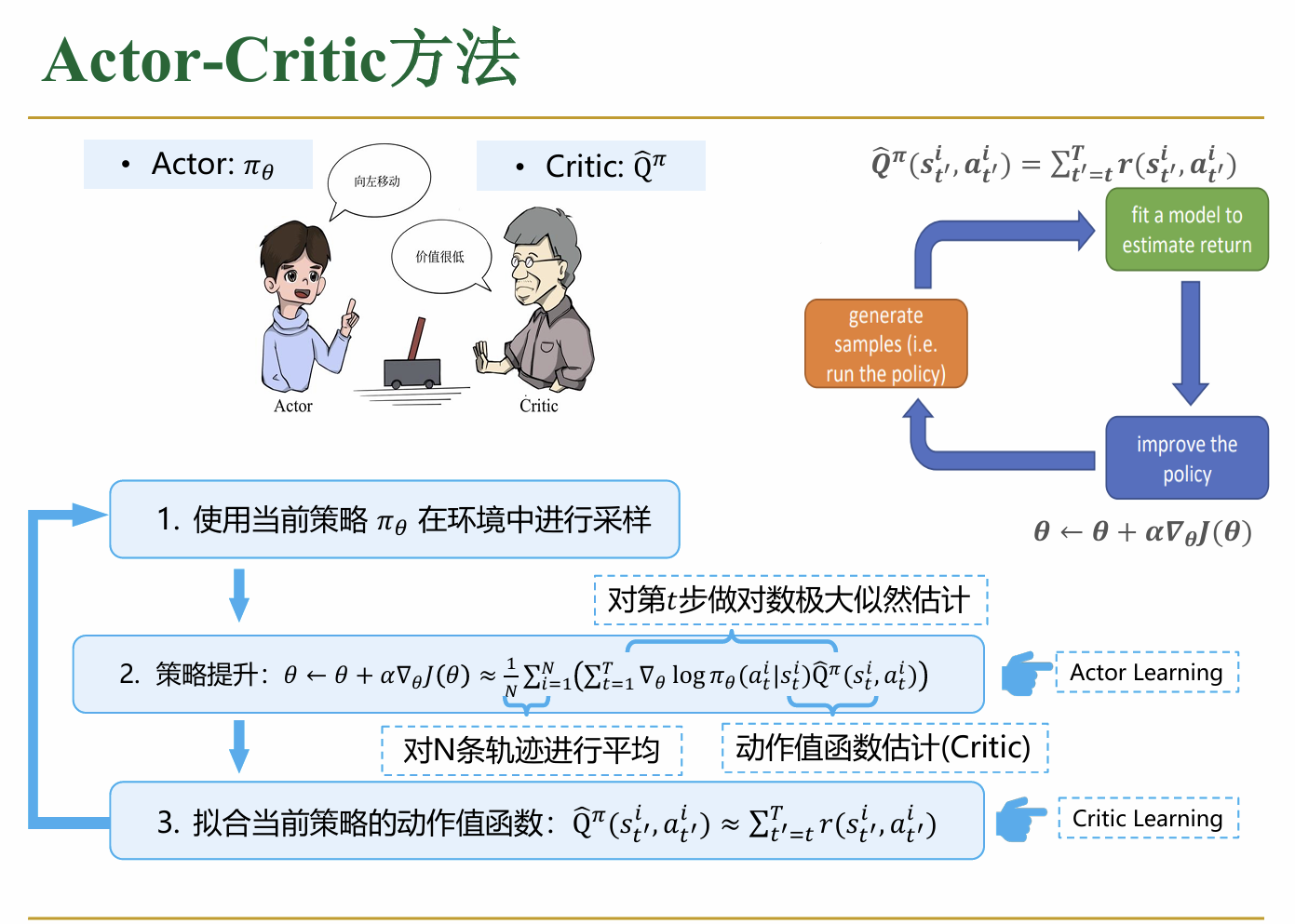
在这个系统中，有两张神经网络 （1）actor网络，这个网络负责“表演”，也就是说，这个网络按照当前的策略在环境中采样 （2）critic网络，这个网络负责“评估”，也就是说，这个网络在当前的策略下，评估当前状态的“价值” actor-critic算法实现过程分为以下几个阶段： （1）首先，随机初始化参数θ（actor网络的参数）以及critic网络的参数 （2）然后根据当前的π(θ)，在环境中进行采样，在这个例子中应该是采样了N个episode （3）在每一步中，Critic网络更新自己的参数，使得其对于Q值的预测与真实值的差距越来越小 （4）之后，利用Critic评估得到的Q值，结合策略梯度算法更新actor网络的参数，再如此循环。
1.3.3 A2C算法
A2C算法（Advantage Actor Critic）是Actor-Critic算法的一个变种（升级）其与前面内容一个基本的区别就是其对于梯度的计算做了一个改进：
（感觉有点类似于前面对REINFORCE算法改进减掉的一个均值，这里相当于是用当前特定动作的期望reward减去了这个状态下的平均期望reward；好处同样是可以降低方差，并且更加明显增加好动作、减少坏动作的概率（由于这样一来，低于均值的动作对应的参数会减小，反之才会增加） 并且，在具体操作的时候，注意到状态转移的公式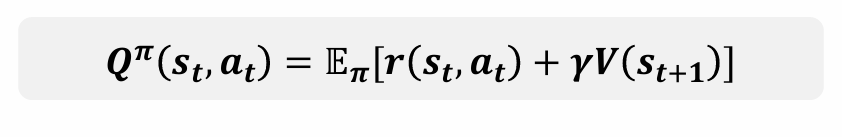
因此，实际上只要维护一个关于V的神经网络来更新各个状态对应的V值就可以了，具体如下：
一个完整的deep A2C的过程如下：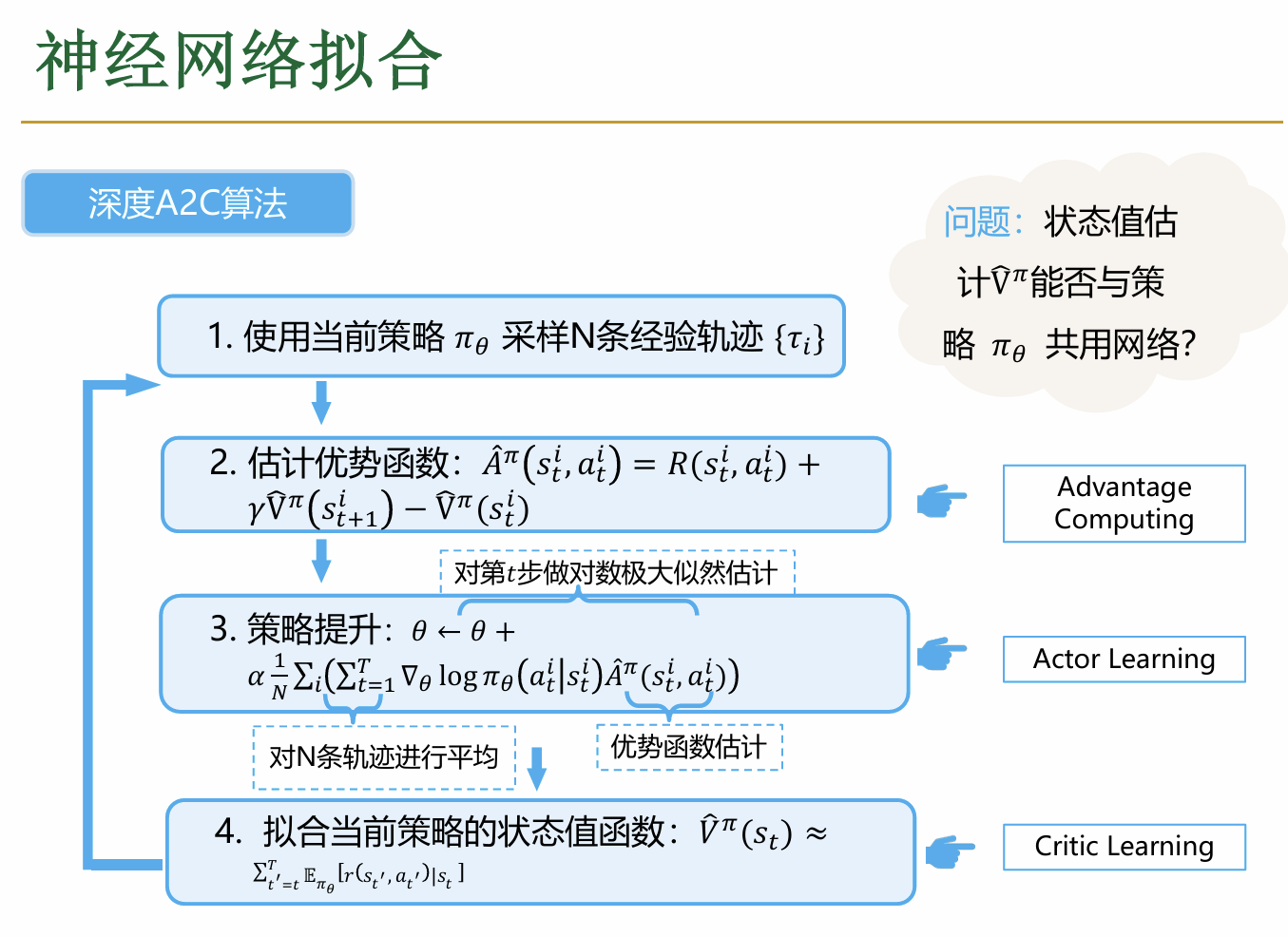
其中，对各个部分梯度的计算根据链式法则蕴含在神经网络各个部分中，一般地最后一步会通过一个softmax进行计算
关于A2C批次更新优化和A3C的内容暂时先略过了
学完了这部分内容，如果向没有学习过这部分知识之前的我介绍什么是策略梯度？或许我会说：这就相当于你先去玩游戏，做出了一系列动作，得到了一系列的奖励（和惩罚）；之后，自然会想要修改策略（的参数），使得好的动作发生概率提升，而不好的动作概率降低。 而在这个基本想法的基础下，策略梯度算法就是让你沿着梯度方向修改这些参数，这样可以最高效地学习。并且，在前面环境已知的情况下，直接根据价值来调整行为显然是容易的，而这里体现的就是一个面对未知情况随机初始化值，然后不断更新的过程。
对这部分内容的补充说明： 1. 对于策略梯度的积分计算的证明是十分复杂的，并且上面的式子也不是非常严谨，在实操中，关键点其实如下所示：
也就是说，我们的reinforce和A2C算法实际上就是用了两种不同的方法来估计这个Qπ(s, a)，前者用实际观测的回报来近似，而后者使用了一个网络来维护这个值。 2. 再详细讲一下A2C中的价值网络：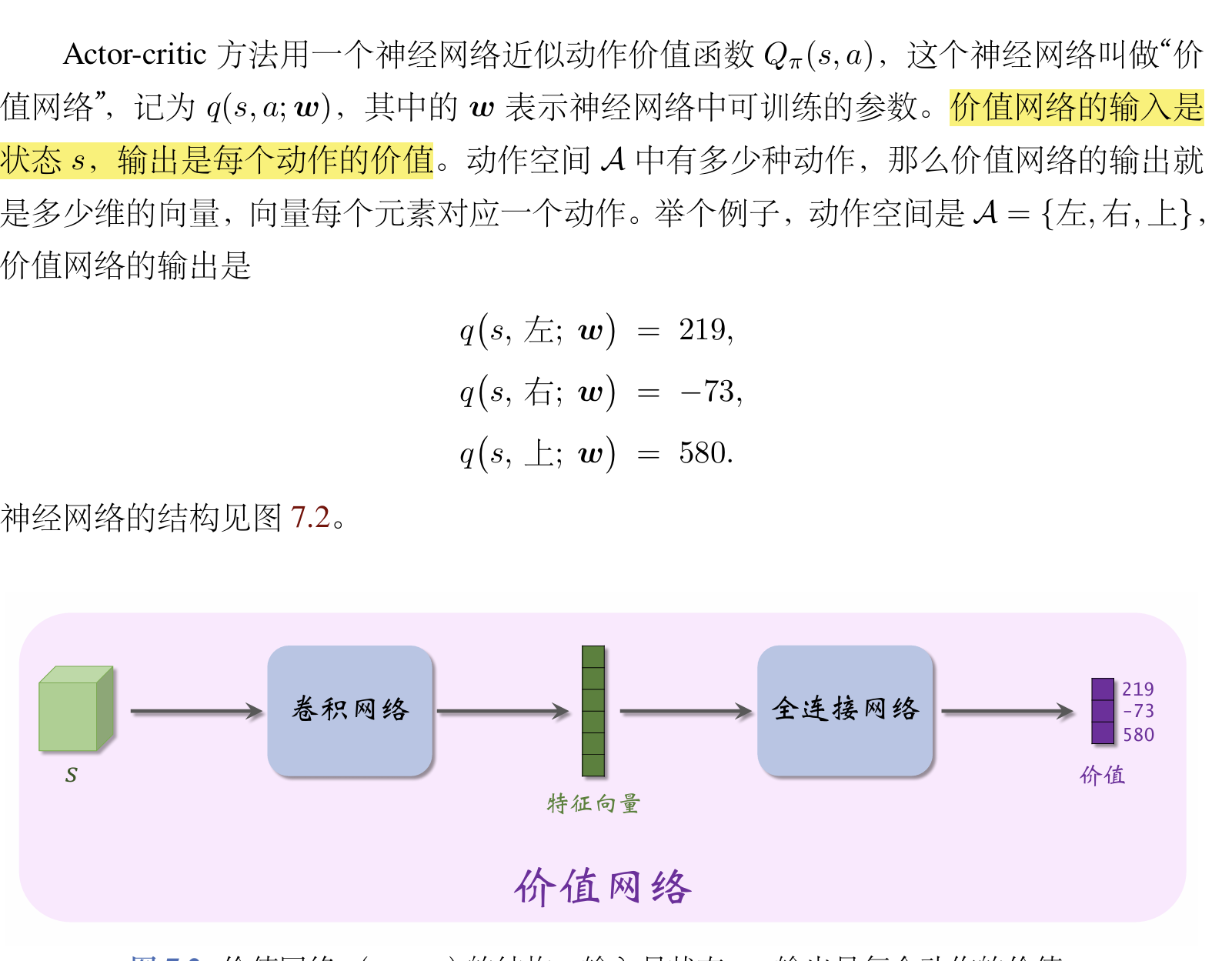
也就是说，其根据具体的某一个输入的状态会输出这个状态下各个行为的价值。 A2C的核心如下：
具体的训练流程如下：