计算理论 CH1
CH1: Sets, Relations and Languages
1.1 Sets
learn some English： 1. proper set 真子集
partition 分割（不相交的分解）
one-to-one function 单射
onto function 满射
one-to-one correspondence 一一映射
1.3 Special Types of Binary Relations
1.recall：symmetric & anti-symmetric:反自反意思是，如果a->b(a!=b) 那么就不能有b->a
2.partial order 偏序：自反，传递，反对称（有大小关系）
3.recall： 在一个偏序关系中的a： least element：对所有的b，都有a < = b，也就是说要比每一个都小才是least minimal element：如果a < = b，那么a = b，也就是说只要找不到比a更小的那么a就是minimal 因此，least更严格，因为要对每一个元素其都要在它的左边。类似地，定义了greatest和maximal
4.total order 全序 指的是在一个偏序关系中，对于任意一个pair(a, b)，要么有a < = b，要么有b < = a；也就是说，所有的都得连起来，两两之间必须可以比大小
5.equinumerous（等势） 如果两个集合等势，那么存在他们俩之间的一个双射。等势关系“~”显然是一个等价关系
6.等价类组成一个分割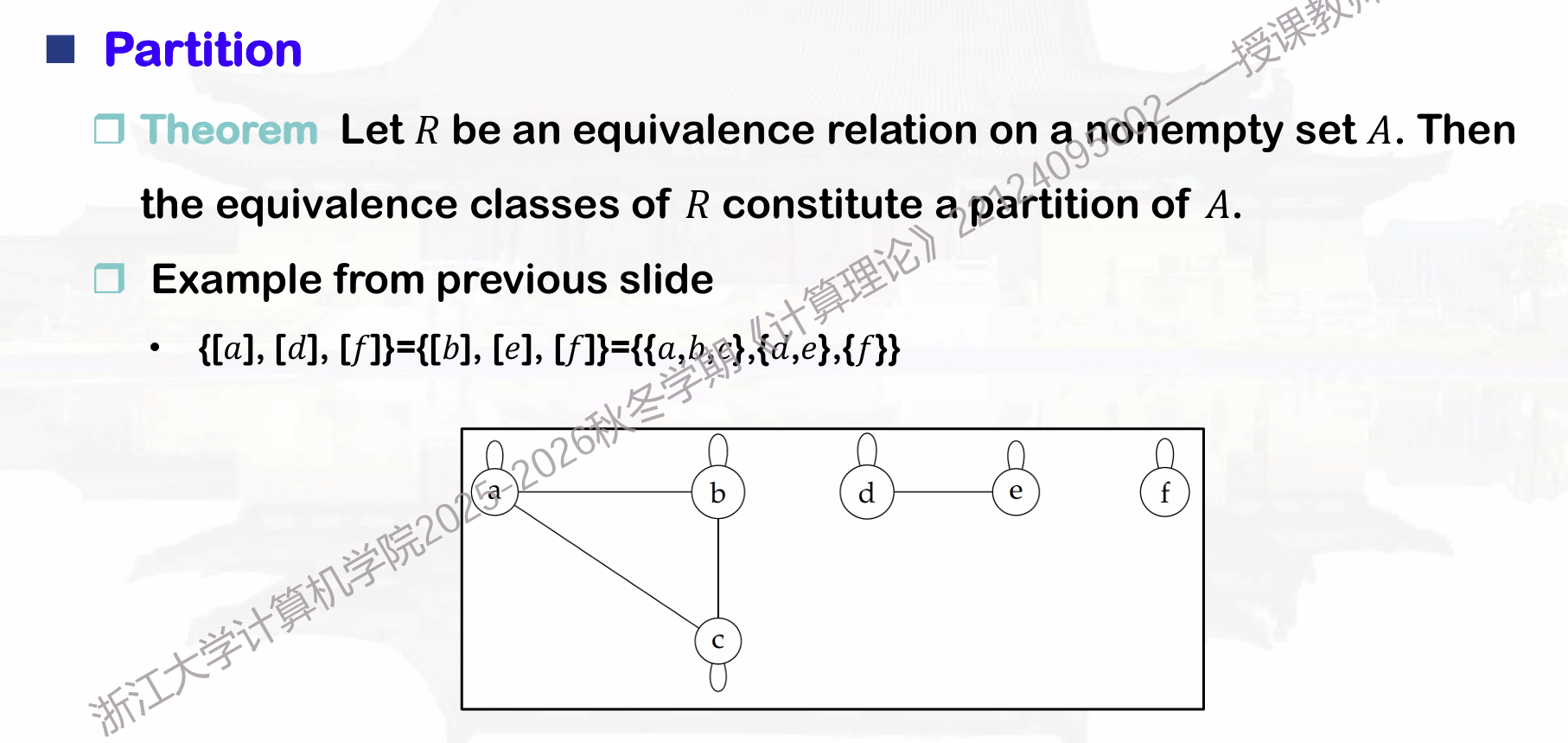
1.4 Finite and Infinite Sets
Cardinality（基数）：集合的基数，也就是集合中元素的数量。等势代表 |A| = |B|。 无穷集合也有基数，使用定义好的符号表示 进一步地，recall finite/infinite set, countable/uncountable finite
这个很好地说明了可数个可数是怎么count的：构造全体质数的幂就可以一个例子：证明N * N是countably infinite的
方法3显然是最容易想到的，也就是说，解决这类方法最好的方法有两种： （1）对于A和B，分别构造出A到B和B到A的单射即可 （2）直接从card大小出发，card介于两个可数集之间的一定是可数的Continuum hypothesis（连续统假设） 说的是没有集合的Cardinality在N与R之间
Cantor’s Theorem
我们不讨论不可数无穷的幂集
对于有限集合的情况，这个定理是显然的（直接算出来）；而对于无限个元素的情况，一方面，说明|A| < = |P(A)|是显然的，因为幂集中包含了原来的每个元素的集合，即对每个A中的x，P(A)中一定有元素x 因此，我们现在只要说明|A|！ = |P(A)|，也就是构造的映射一定不是满射，P(A)中一定有元素指不到。这里我们使用反证法：
具体解释一下这个证明：首先假设f是一个满射：
（1）集合B的意思是：B中是A的一些元素，在我的映射f规则下，B中的元素x满足f(x)中没有元素x。比如说，f(1)={1,2,3}，那么1不属于B；f(2)={3,4,5}，那么2属于B。
（2）然后根据定义，集合B也一定同时是幂集中的一个普通元素，因此存在一个t，满足f(t) = B。然后分情况讨论都会得到矛盾。这是一个更清楚的版本：
1.5 Three Fundamental Proof Tech.
数学归纳法；抽屉原理；对角线原理
1.5.2 The Pigeonhole Principle
在这门课的特色下，这个原理的如下描述：
一个有趣的例题 
核心在于想到“两个点确定一个大圆”，剩下就很简单了
1.5.3 The Diagonalization Principle（对角线定理）
定理的描述如下： 
具体解释，也就是说在一个A上的二元关系R：
D中收集的是所有在对角线上但是不在R中的元素：比如说R中有(a,a)但是没有(b,b)，那么b在D中。
同时定义一个Ra:如果R中有(a,x)，那么Ra中包含x。
这个定理说的是：对于每个A中的元素t的Rt，其与D都不同，结合上面的例子可以直观理解
其实对角线原理的原理很显然：比方说上面这张表，我的a d f对角线是空的，如果有一行的元素恰好要是a d f，那么首先它不可能是第a d f行，因为他们对应的(a,a) (d,d) (f,f)是空的；而对于其他的任意第i行，由于(i,i)上是满的，所有其不可能仅仅含有a d f
1.5.3.1 对角线原理证明康托定理
对于康托定理后面证明其不是满射的部分，我们如下证明：
1.5.3.2 对角线原理证明|R| > |N|
表述起来就是：建立N到R的映射，说明这个映射一定不是满射。在现在已经建立的映射上，选取一个新的有理数d，第一位和第一个不一样，第二位和第二个不一样，……，那么其和之前映射中每一个R的数都有一位不一样，因此和他们都不一样。
如何体现对角线原理？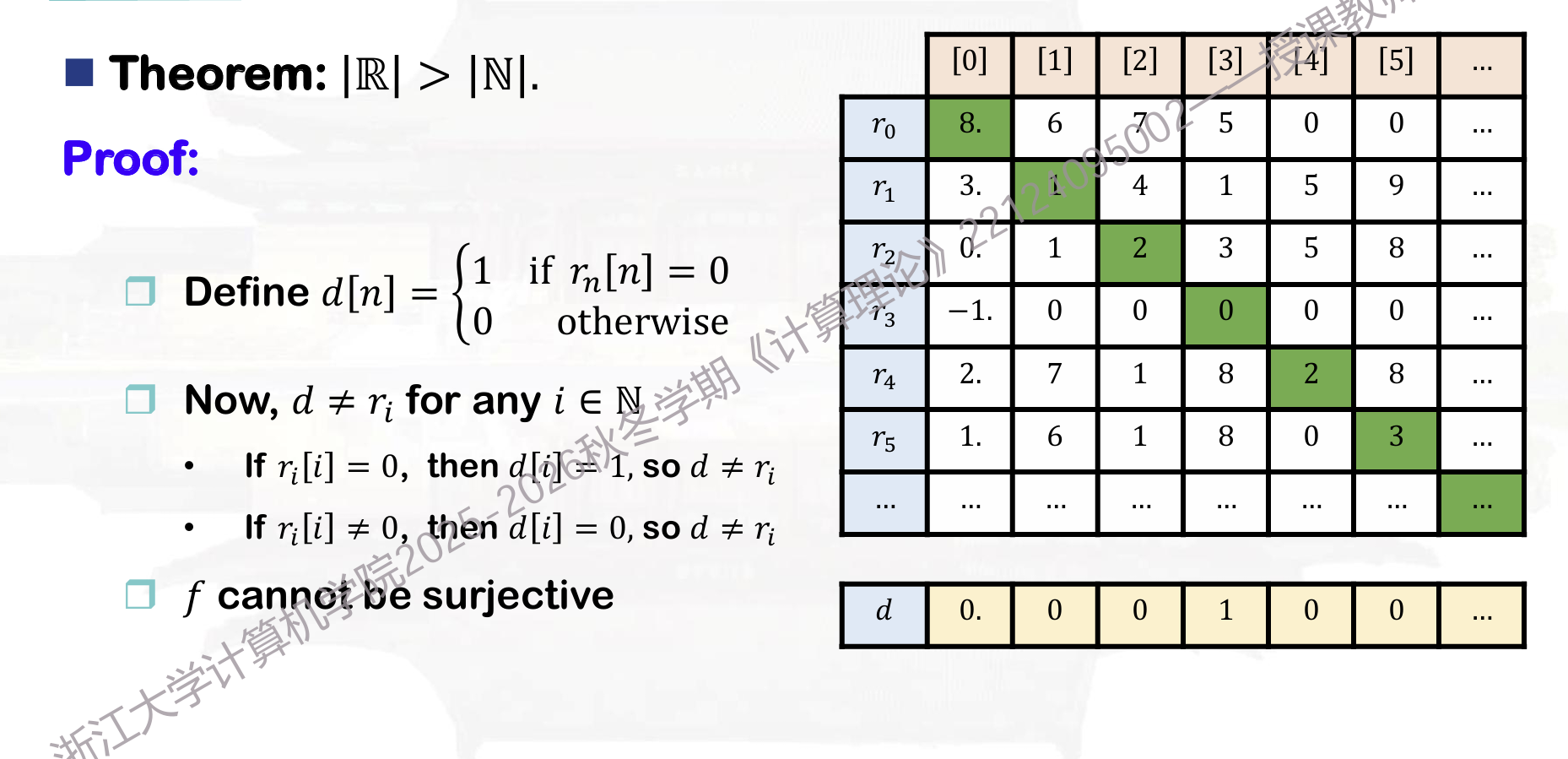 
相当于，我们这样理解：对于每一个无限不循环小数取其对角线，如果对角线的值为0，我们认为其是“没填”；否则就认为是填了数字。那么对于这个对角线（实际上就是一个0，1的无限小数），其与表中的任意一个值都不同，因此不是满射。
相信这很容易看出：对角线原理用于反证一个映射不是满射构造反例的威力很大，证明的关键点在于如何选择表格的规则。
1.6 Closure（闭包）
闭包一定要和具体的二元关系放在一起说才会有意义
1.6.1 closed（封闭的）
也就是说，对于一个集合A和一个二元关系t，如果A上的任意两个元素计算后还在A中，那么其对于A是封闭的。
那么，若B为A关于关系t的闭包，指的是：B是满足对于关系t封闭且包含A的最小集合
比如说，加法对于自然数是封闭的，但是减法不是，对于减法而言，N的闭包就是整数集Z
1.6.2 recall：传递性、自反性、对称性的闭包
1.6.2.1 reflexive, transitive closure
由于反射性和传递性很多时候结合在一起才有完整的功能，因此将他们两放在一起构建闭包。对于一个集合R，其reflexive, transitive closure记为R*，定义如下：
也就是说有路径可以连起来的两个点就要添加到二元关系中，当然一个点和自己也要算在里面
1.6.2.2 transitive closure
其实没啥东西，理解闭包定义就行，记为R+(?)
1.7 Alphabet and Language
1.7.1 Alphabet 字母表
具体的定义如下：
也就是说，任意有限集都是一个alphabet，通常用Σ来表示；alphabet中的元素叫做symbols
1.7.2 Strings
这个问题不成立，因为其中一定有一个代表空字符的e,也就是说，如果我的alphabet是空集，其中也一定含有e这个string 对于一个字母表Σ，一个string就是其中元素组成的有限长序列
1.7.3 Operation of strings
为了方便理解，可以把一般的字符看成有意义的，而empty string看作“1”
1.7.4 Language：Set of Strings
也就是说，“语言”是针对一个字母表而言的，是一系列string组成的集合，也就是说其为Σ*的一个子集