RL5：策略梯度进阶；策略优化算法

RL5：策略优化算法

对前面一章内容的补充，以及引入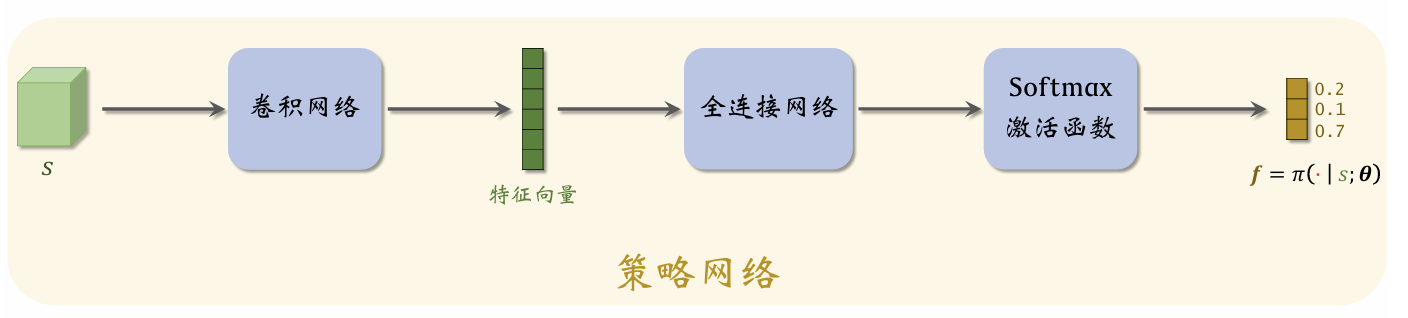： 如图为策略网络，如果输入的为向量那么省略前面两层；否则，可以利用卷积网络先将张量转化为特征向量，然后接入全连接网络。

5.1 TRPO

TRPO 的全称为Trust Region Policy Optimization，中文翻译为信任区间策略优化。TRPO算法具有两个很明显的优势：其表现更稳定、对学习率不敏感，并且其需要的训练经验更少。

5.1.1 置信域方法

理解TRPO的基础就是这个所谓的置信域方法。置信域的概念最先在优化问题中提出，比如说想要利用θ来优化J(θ)，一般来说优化过程是不断更新当前的θ_now。对于置信域方法的具体描述如下：也就是说，在这个参数θ的邻域内，我们构造了这个一个函数L，使得在这个区间上可以用L来替代J；置信域需要伴随着构造的函数一同存在才有意义。 置信域方法的意义就在于，大多数时候我们的目标函数J(θ)形式上会很复杂，但是如果我们能找到一个可以值得我们“信任”的形式上更简单的函数L(θ)，那么我们就可以直接优化这个函数来达到目的即可。 所谓的置信域方法的核心在于如下的两个步骤： 1. 给定θ_now,确定使用的邻域，找到用于近似的函数L 2. 在这个区间内，优化参数θ = argmax(L(θ))，这个θ就是这一步优化得到的θ_new。随后重复这两个步骤，继续优化的过程。

5.1.2 数学推导

TRPO的核心在于如下的几个等式：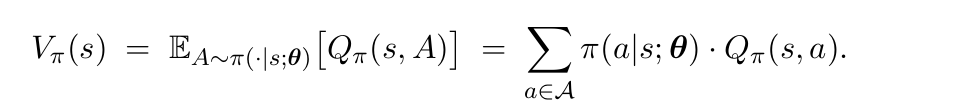

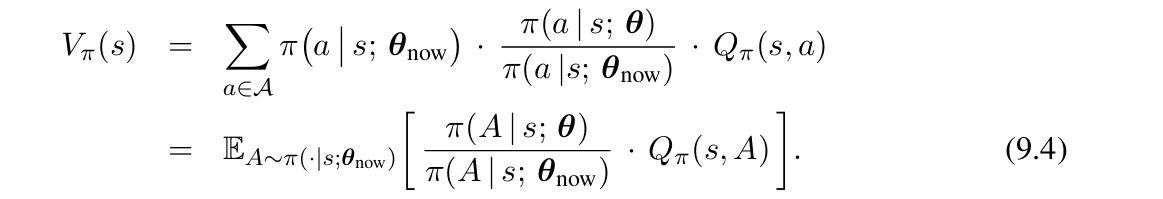
第一个式子就是把一个状态的价值拆分成各个动作的期望回报的加权和； 第二个式子在分子和分母上同时拆出了一项π(a|s; θ_now)，然后把总的期望项改成了关于现在参数θ_now的期望项； 第三个式子就是由于J(θ)是关于所有状态的期望和，根据第二个式子简单变形得到。 但是，在具体的操作过程中，肯定要做一些近似工作，这里我们外面两项的期望分别是对状态和动作而言的，因此我们尝试使用蒙特卡洛方法进行模拟时，采取这样的方法：我们使用当前的策略θ_now完整地玩一局游戏，会得到一系列的动作-状态-奖励序列。由于每一个状态都是从环境中观测到的，而动作也是按照当前的策略进行选择的，因此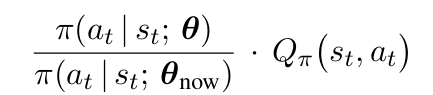就可以看成是9.1式子的无偏估计。因此，对于以上的这个结果进行n项的求平均，就也是一个无偏估计。因此综上，得到如下的内容： 但是，由于对于环境的未知性，这里的Q_π还是不方便求出，因此还需要对于Q进行估计。在一个置信域中，可以如下的方法进行两次估计：因此，最后的最后，在我们的置信域中，有如下的估计成立，这就是我们接下来需要优化的函数。

这里对于Q的第二步近似，是把新参数的新策略近似为了旧的策略，因此这个强调了置信域的重要，不然这个近似的差距会很大。

5.1.3 最大化

最大化的过程很显然如下：

5.1.3.1 置信域的选择

对于置信域的选择，主要有两种主流的方法： 1. 选择一个以当前的θ_now为球心的高维球，也就是说：选定一个半径,问题转化为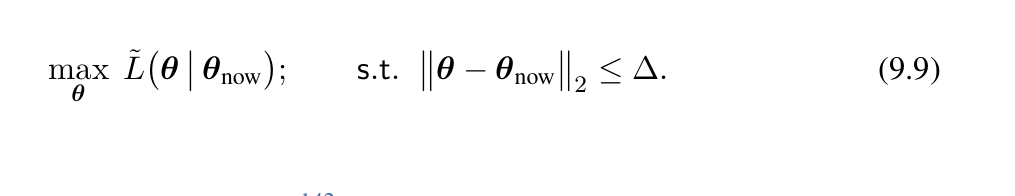： 这个方法的好处是置信域十分简单明了，但是实操起来效果并不是很好 2. 第二种方法是借助KL散度的方法。

KL散度具有如下的定义：

从这个定义就可以看出，这十分直观：我们需要限制选定的基点θ_now与我范围内的θ形成的策略的散度值相差不能太大，否则的话我的策略就会有很大的偏差，L的估计值便显得不合理。数学地写出来如下：

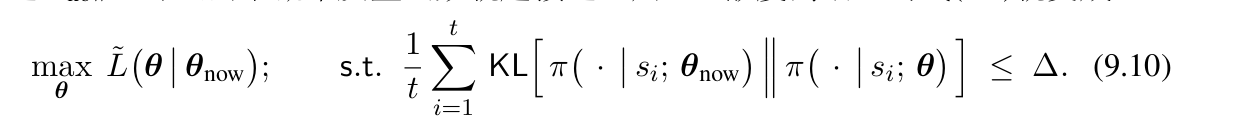
5.1.3.2 如何计算？

信奉这样一句话：也就是说，会有具体的计算方法，了解到这个程度就够了（）

5.1.4 训练流程总结

这里也说到，TRPO算法虽然理论很先进，具有很多优点，但是由于上面带约束优化问题本身的复杂度，导致其真正实现起来还是有一定的困难。

5.2 PPO

PPO的全称为Proximal Policy Optimization，中文意为近端策略优化。 从我自己先前的感觉来看，PPO应当是目前应用最多、效果也最好的一个算法了。事实上也是如此： “PPO（Proximal Policy Optimization）是OpenAI在2017年提出的一种强化学习算法，该算法在目前强化学习领域中具有较好的效果与算法稳定性，是应用最广泛的强化学习基线算法之一.” 对于这个算法的学习，最好的资料是参考spinning up关于PPO的内容 ### 5.2.1 核心思想 PPO算法的核心思想与之前TRPO中的置信域一样，PPO算法也希望在每次更新的过程中对于当前策略的更新在一定的范围内（也就是说，不发生过大的变化），而对于这个的衡量一个很好的方法就是新策略和旧的策略下动作概率的比值。 但是，在TRPO中，无论是使用球型置信域还是KL散度，其都是一个带有约束条件的二阶优化问题（也就是在解决的过程中必须要求二阶导才能解决）。为了应对这个不足，PPO算法采用的解决方法是引入一个剪切目标函数，来限制策略不会发生剧烈的变化。

5.2.2 具体数学方法

延续之前的定义，同时记$r_t(\theta) = \frac{\pi_\theta(a_t | s_t)}{\pi_{\theta_{\text{old}}}(a_t | s_t)}$

首先介绍所谓的clip（剪切）方法：首先引入一个clip()函数（把它看作是函数：对于我的目标量r_t(θ),首先我设定一个适当的超参数ϵ，如果r_t(θ)落在范围[1 − ϵ, 1 + ϵ]之内，那么保持其值不变；否则，超出范围，那么截断其值到边界。

比如说，我设定ϵ = 0.2，那么对于r_t(θ)，如果r_t(θ)在范围[0.8, 1.2]之内，那么保持其值不变；否则，比如r_t(θ)为0.5，那么截断其值到边界为0.8;若其值为1.5，那么截断其值到边界为1.2。

具体分类讨论后，下面的这张图比较直观：

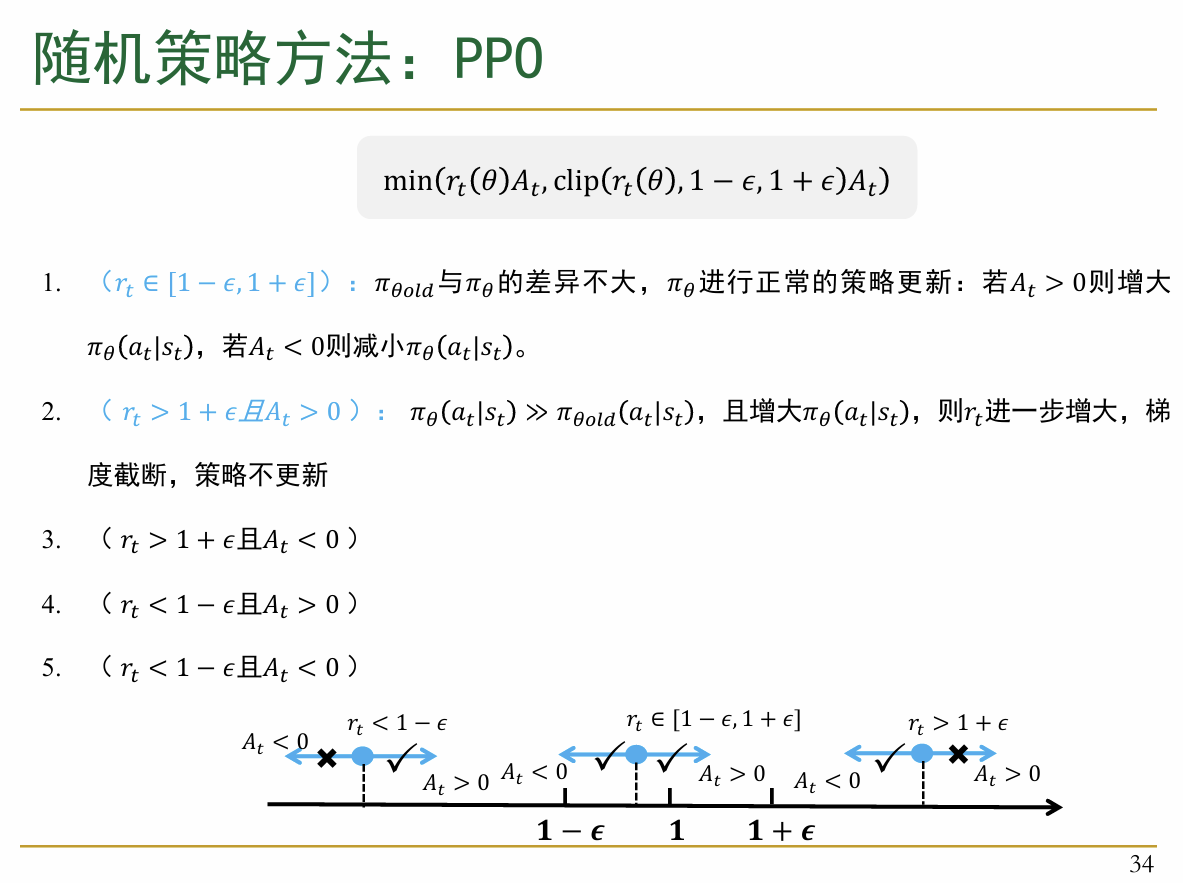
PPO算法更新的目标函数如下： 其中，A的定义和之前一样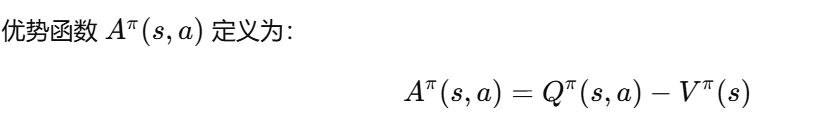：为当前策略下采取特定动作的奖励减去这个状态期望的奖励

一个易于代码进行处理的版本如下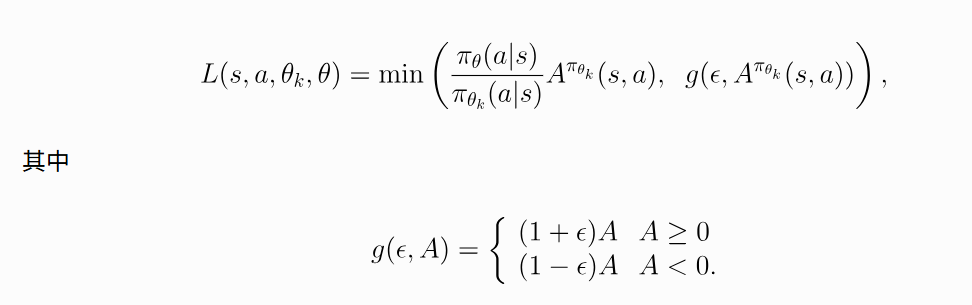： 相当于把后面clip的部分简单粗暴直接赋值限定为两个端点的值

这样看就很直观：如果优势函数A > 0，就说明当前的策略会更好，但是更新的幅度被限制在1 + ϵ的范围内；也就是说，过度偏离策略不会使你受益。A < 0的情况相应地也同理。

5.2.3 伪代码实现

关于PPO的源代码 对于伪代码，整理了一下，更完整一点的解释如下：