RL1：强化学习基本概念，马尔科夫决策过程，DP
# RL1：强化学习基本概念，马尔科夫决策过程，DP
1. 基本定义
- 强化学习是机器学习的一个分支，专注于让智能体（Agent）通过与环境的交互学习最优策略，以最大化累积奖励。其核心思想是试错学习（Trial-and-Error），类似于人类或动物通过经验改进行为的过程。
强化学习的主体为智能体(agent)，即为对环境做出感知、决策、行动的对象 （e.g. 玩游戏时的角色&自动驾驶的汽车）；环境(environment) 是与智能体交互的一切外界规则与机理 （即为智能体所处的“世界”），
Q: 价值学习和策略学习分别是什么？
A:（以后慢慢补充）
2. 马尔科夫决策过程(Markov decision process，MDP)
2.1 MDP基本五要素
MDP是可以通过强化学习解决问题的基础建模，其由以下的五个元素组成𝑀 =< 𝑆,𝐴,𝑃,𝑅,𝛾 >
- 状态（State）集合 S: 状态指的是当前时刻，对于整个环境一帧画面的概括 (e.g.下棋一个时刻棋盘所有棋子的位置&玩游戏时某时刻的一帧画面)
- 动作（Action）集合 A: （我认为）动作必须依赖于特定的状态，动作集合是agent在当前状态下可能做出的所有决策
- 状态转移函数P: 状态转移取决于当前的状态和行为，并且具有随机性，概率用状态转移函数 𝑝(𝑠’|𝑠,𝑎)进行衡量，指的是agent在当前状态s采取行动a转移到状态s’的概率。
要注意状态转移具有随机性，由于环境的不确定性和干扰，当前agent即使在给定时刻采取确切的行为，也无法确定下面的状态。下面是一个通俗的例子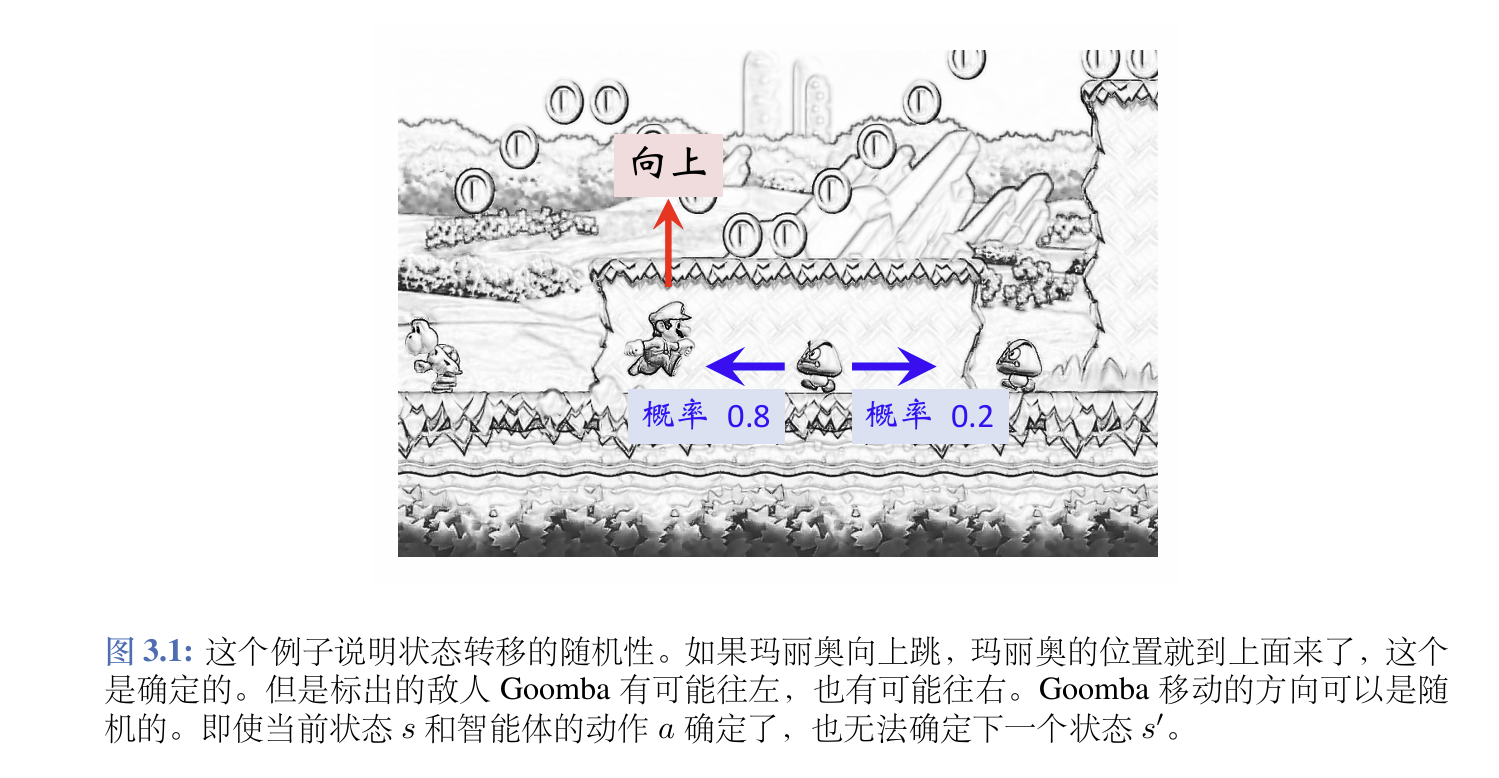
- 奖励函数R: 人为设置的奖励对于训练模型很重要，通常来说需要设置一系列的r(s,a,s’) (从状态s采取行为a转移到状态s’的奖励) 给智能体，以达到最终的训练目的；有时奖励会退化为r(s,a)
Rt与r(s, a)的区别：
依旧让gpt来说： > r(s, a): > 表示 某个状态下，执行某个动作后得到的即时奖励。 它更像是一个 奖励函数，给定状态 s 和动作a，返回一个奖励值。 它是环境对动作的即时反馈，通常与时间步无关。
rt : 表示在 特定时间步 t 下，智能体执行某个动作后得到的即时奖励。 它是 即时奖励的时刻标记，指在时刻t 上的反馈。 这个奖励可能与某个特定的状态或动作有关，通常用于标识当前时间步的奖励。 所以说，主要就是衡量的参数不同（状态、行为 or 时间）
缺一个MDP矩阵形式的解，但感觉没啥用，以后再补充
- 折扣因子𝛾: 一个介于0和1之间的参数，由于（人之常情）需要多关注眼前立刻获得的回报，因此对于未来若干步之后才能取得的好处就要设置折扣因子来减小权重
2.2 回报，价值函数，策略
首先说明回合(episode) 的概念：一个“回合”指的是智能体从初始状态与环境交互直到terminal state的过程，就是 一局游戏，一次任务从开始到执行结束.
回报（reward）: 回报 Gt 实际上是一个统计量，指的是一个回合后（一局游戏结束后），由于所有经过的状态、行为和每一步的奖励都确定了，Gt 统计了整个回合（或者有限视野内）从t时刻开始所有奖励的累计值，即为
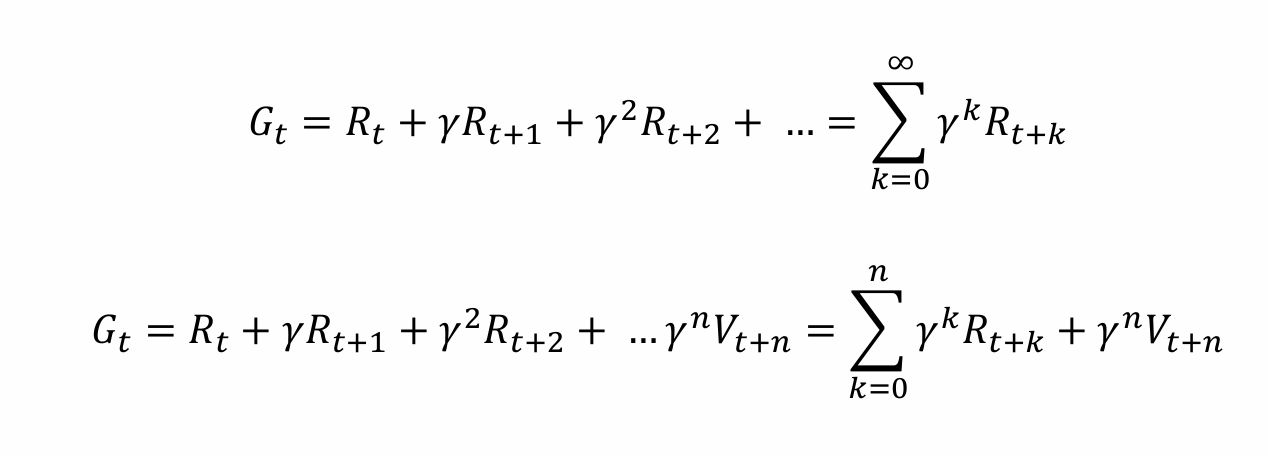因此，回报是一个确定的值价值函数: 一个状态的期望回报即为这个状态的价值；价值函数 V(s) 输入一个状态，输出这个状态的期望回报；价值函数可以写为 V(s) = E[Gt|St = s]。进一步地，将其展开得到：
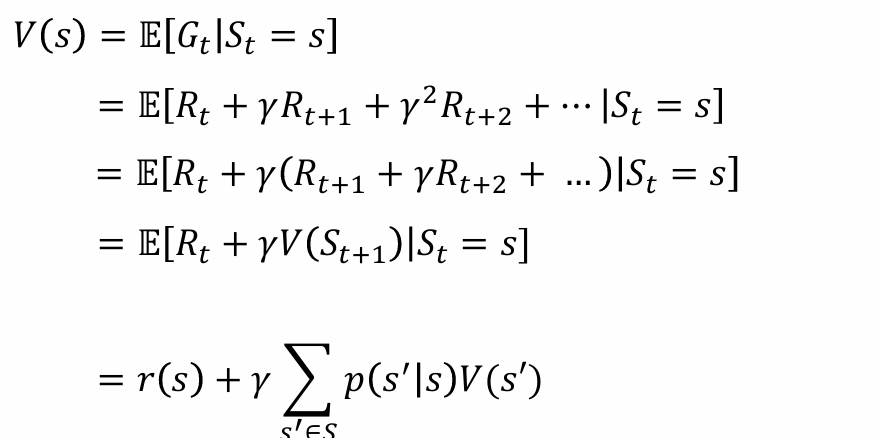
对于价值函数的定义式，在引入策略 π之前，感觉有些抽象，因为状态转移之间没有规律可寻，gpt这么说： > 在 强化学习 或 马尔可夫决策过程（MDP）的背景下，价值函数 𝑉(𝑠)主要用来评估每个状态的“好坏”。如果没有显式的策略𝜋，通常假设状态值函数 V(s) 是在某个默认策略下定义的，或者更常见的情况是我们关心的是最优策略。
因此，我觉得V是用来衡量状态“好坏”的抽象概念，具体要结合策略才有实际作用
- 策略(policy), π 策略是智能体通过判断环境和状态，来决定下一步动作的函数。通常来说，策略分为确定性策略（一个状态对应唯一的动作：比如说，走迷宫设定策略为一直往前冲，除非看到墙就直接右拐）和随机性策略。在机器学习中，我们主要讨论随机性策略。 在随机性策略中,核心内容为概率密度函数 π(a|s) ，其得到的结果为一个概率分布，为在当前策略&状态s下，采取动作a的概率，即 P(at = t|st = s)。
采样(sample) 和 轨迹(trajectory) 是另外两个比较重要的概念。gpt这样告诉我： > 在 强化学习 中，采样（sample）指的是从环境中收集单一数据点或一小段数据。通常来说，采样是从当前状态中通过采取一个动作获得的反馈信息。这些数据（状态、动作、奖励、下一个状态）通常是通过与环境交互而获得的一个时间步的数据点。每次从环境中收集到的一组（状态、动作、奖励、下一个状态）就是一个 采样。 轨迹（trajectory）通常指的是智能体从某一初始状态出发，通过多次采样所得到的一系列数据点。它是智能体在一段时间内与环境交互的整个过程。
2.3 V与Q, Bellman
- MDP的价值和回报：结合上面给出的策略概念，在使用策略π的前提下，我们很容易得到在相应策略下一个状态价值函数 Vπ(s)的表达式
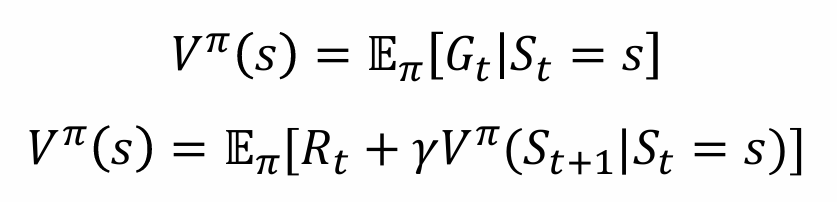进一步地，定义价值-行为函数 Qπ(s, a)，指的是agent在采用策略π的大方向下，在当前状态s已经采取特定行为a之后，期望得到的总回报。
V与Q的关系
根据上述的定义，可以比较容易得到V与Q之间的计算关系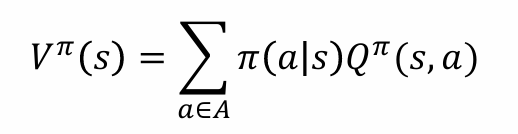
通俗地说，在给定的策略下，V为给定状态s的期望价值，Q为给定状态s和行为a的期望价值；因此V即为π的概率分布下各个行为期望价值的加权和。 从另一个角度看：
就是拆一步当前行为、状态的即时奖励，再加上当前(s,a)转移到各个新状态的V回报的加权和。（当然还有γ） 简单来说，V和Q都是回报，只是涉及的变量不同
5.贝尔曼期望方程，贝尔曼最优方程：策略评估与策略优化 （1）贝尔曼期望方程：
数学上来看，贝尔曼期望方程就是根据上面V与Q的关系转化为只有V和Q的形式。我理解其本质是一个“向后迭代一步”的方程，其将最后的回报转化为仅仅与下一步所有回报值的加权平均，同时也方便迭代递归求值 （2）贝尔曼最优方程：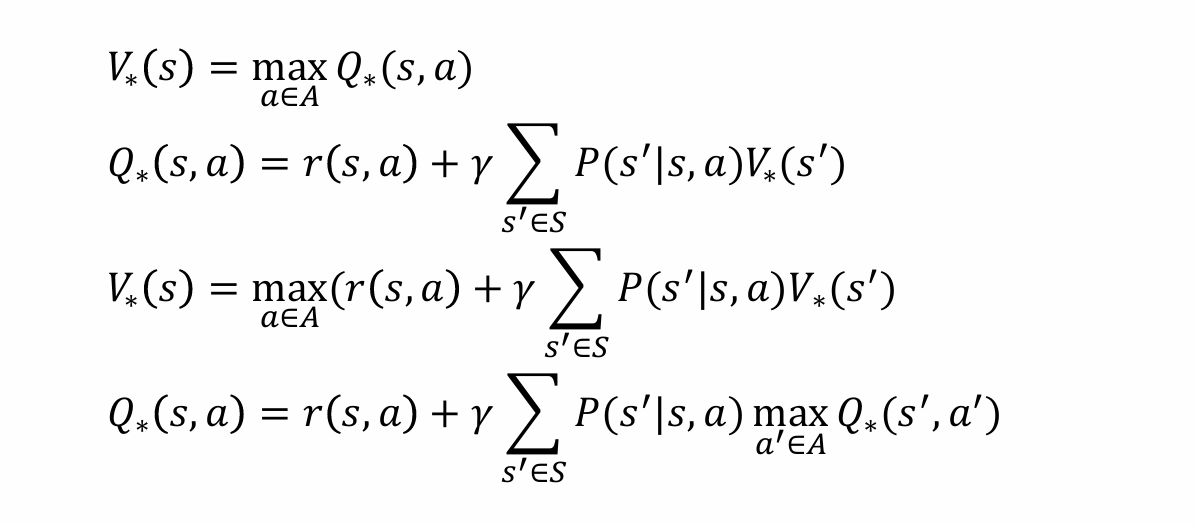
如果说贝尔曼期望方程是针对当前的策略计算值，那么贝尔曼最优方程是仅仅关注最优值，即在迭代过程中，不关心策略，而是每一步贪心，选择能让下一步回报最大的动作。
3. 动态规划(dynamic programming)
3.1 introduction
在RL领域，动态规划主要用来解决一类已知环境模型的问题，结合上述的贝尔曼方程与DP的将全局寻求最优转化为每一步寻求为最优的思想解决问题。（后面会很容易看出为什么要这样） 首先定义一系列符号： 状态集合表示为 {0（终止状态）,1,2…n}，每个状态对应的可选动作集为 A(i) pi, j(a) 表示在状态i,采取行动a转移到状态j的概率，ri, j(a) 表示在状态i,采取行动a转移到状态j的奖励，（前面还有k步后的折扣因子γk）
动态规划期望得到一个最优的策略，即在每一个状态i下，都能给出一个当下最优的动作μ(i) ∈ A(i)
3.2 基于dp的强化学习算法————Bellman方程的应用
3.2.1 策略迭代(policy iteration)
对于策略迭代，一般分为如下的两个步骤交替进行
第一步的 策略评估 中，采取当前的策略，一般会为所有的状态定义一个（随机的）初始V值，之后不断使用Bellman期望方程进行迭代，直到收敛为止，以得到各个状态真实的奖励V值。
初始的策略应该可以完全随机设置；初始的V值感觉也可以随机设置，是否有影响存疑（我觉得无所谓）；同时，强大的Banach不动点定理保证一定可以得到最终的收敛解决；如下的简单推导确保优化结果一定越来越好
更简单地说，贝尔曼方程就是用来求出V值，然后根据V求出所有的Q值，最后根据Q值来更新策略
初学时陷入了一个误区：既然算出V后可以得到获得最好Q的行为a，那为什么不直接选择这个行为作为最佳策略？ 其实也很简单解决，因为这只是目前π看到的所谓好行为，但对于别的策略并非最优
3.2.2 价值迭代（value iteration）
核心表达式为 $V(s) \leftarrow \max\limits_a \left[ r(s, a) + \gamma \sum_{s'} P(s' | s, a) V(s') \right]$ ，通俗说，策略迭代需要计算所有行为得到的奖励再加权相加作为当前状态的V，而价值迭代直接把奖励低的pass掉，直接把奖励最高的按100%权重给当前的状态。 就这样，得到新的一轮V，重复这样的方法直到得到的V收敛即为最终确切的状态，然后再根据 $\pi^*(s) = \arg\max\limits_a \left[ r(s, a) + \gamma \sum_{s'} P(s' | s, a) V^*(s') \right]$ 反推出策略即可
总结一下Bellman方程与DP: 结合具体的例子看Bellman方程比较好理解，期望方程就是把所有对应的Q(s, a)加权得到新的V值，而最优方程就是把结果最好的Q*(s, a)直接作为新的V值；第一种方法对应不断迭代得到收敛的V值再进行优化的策略迭代算法，而由于这个阶段的巨大计算量，价值迭代则直接用最优的替代来节约计算时间。 然而，由于DP算法对于解决问题的要求很苛刻（要求所有的状态转移概率和获得奖励值全部已知），而大多数问题都显然比这个复杂，因此局限性还是很大的。